The simplifying assumption that the economy has, for a long time, been in longrun equilibrium before a monetary disturbance occurs, is not made in this section, and this is because it is a bit restrictive. Thus, the longperiod moving average in (7)( 8) is no longer necessarily equal to the longrun equilibrium exchange rate as in (10).

Instead, it is a function of all past exchange rates, but since this complicates the formal analysis, a small simulation study is accomplished in order to illustrate the behavior of the model. Basically, the equations that are used in the simulations below are the equations that describe the benchmark model, i.e., (1)( 3), the expectations formations, i.e., (4)( 9), and the exchange rate in longrun equilibrium, i.e., (15) and (19). All these equations are reduced to two equations[13] . The first equation is[14]

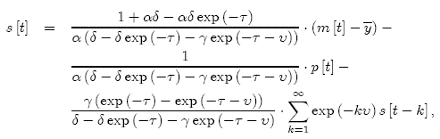(73)

and the second equation is

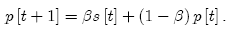(74)

In the previous sections, money supply was exogenously given. This assumption is now replaced with the assumption that money supply follows a stochastic process:

(75)

In contrast to previous sections, the market does not have perfect foresight here, and this is because of the di¢culty in deriving the exchange rate’s perfect foresight path. Obviously, it is not possible to illustrate the behavior of the model from all possible aspects. Therefore, we restrict the illustrations to three cases; a change in the degree of stickiness of goods prices (β), a change in the planning horizon in currency trade (τ ), and a change in the distribution of weights given to current and past exchange rates (ν).

Speci…cally, the degree of stickiness of goods prices is assumed to be β = 0:001 and β = 0:5, respectively, the planning horizon in currency trade is assumed to be τ = 2 and τ = 100, respectively, and the parameter that determines the distribution of weights given to current and past exchange rates is assumed to be ν = 0:001 and ν = 100, respectively. In all three cases, the same time path of money supply is used, where the probability of a change in money supply is 2ε = 0.2. See Figure 1.

The values of all other structural parameters in the model do not change in the simulations, and the number of time periods is 100[15]. See Table 1 for the values of all structural parameters in the simulations, and see Figures 2 Figures 9 for the time paths of the exchange rate.

Firstly, by visual inspection of Figures 19, the exchange rate’s variability is larger than the variability of money supply. This behavior of the model is also consistent with the model’s behavior in the previous

sections, where (10) did hold (assuming equality in the equation), since the conditions for exchange rate overshooting and stability were the same. Secondly, an increase in the flexibility of goods prices (β) has two e¤ects on the exchange rate’s time path. The first effect is a decrease in the exchange rate’s variability, and the second effect is that the exchange rate’s adjustment path is nonoscillating when goods prices are almost completely rigid and oscillating when they are less rigid (e.g., compare Figures 2 and 6). The first effect is rather intuitive since goods prices absorb more of the monetary disturbance and, therefore, the exchange rate need not adjust as much for the economy to reach longrun equilibrium. The second effect is consistent with the model’s behavior in the previous sections (see the discussion in connection with (50)( 51)).

Thirdly, a longer planning horizon in currency trade (τ) decreases the exchange rate’s variability (e.g., compare Figures 2 and 4), and this, of course, is because less weight is placed on technical analysis when forming market expectations. Fourthly, an increase in the parameter that determines the distribution of weights given to current and past exchange rates (v) decreases the exchange rate’s variability (e.g., compare Figures 2 Figures 3), and this is because an increase in the parameter has the same e¤ect, in principle, as a longer planning horizon in currency trade (compare τ and v in (73)). The model’s behavior when the remaining structural parameters (i.e., α, γ and δ) change is not discussed in this paper. Of course, changing these parameters may also generate interesting results.

---

13 (73) below is derived in the Appendix, and (74) below is (3) slightly rewritten.

14 Even if (8) is not explicitly utilized in the derivation of (73), the weights given to current and past exchange rates are still constrained by (8).

15 When deriving the exchange rate’s time path in the simulations, the infinity symbol (∞) in (73) is replaced with 100.

By Mikael Bask and Carina Selander

Next: Concluding discussion

Summary: Index