Definition (Partial Distribution) Let X is a non-negative stochastic variable, and it follows the
distribution of density

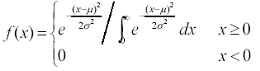(1)

then X is said to have a Partial Distribution, and denotes X e P( µ, σ²).The partial distribution is a kind of truncated normal distribution.

By means of [1], we have

Theorem 1 For any x e [0,∞], the following equations are correct approximately:

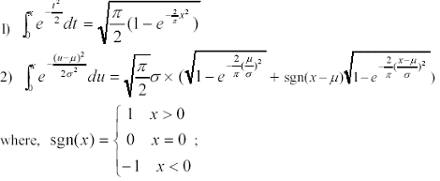
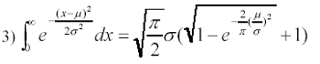
Theorem 2 Let X follow the partial distribution P( µ, σ²), thus
1) The expected value E(x) is as follows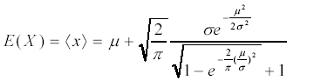(2)

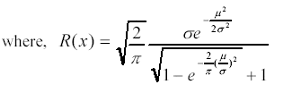(3)

2) The variance D(x) is as follows

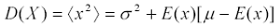(4)

 

Prof. Feng Dai

Next: Properties Analysis

Summary: Index