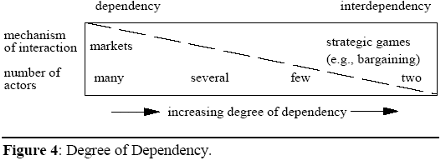
Due to its significance in economics, one structural determinant that deserves special attention is the number of actors.[60] In economics, the mechanism of interaction among individuals (i.e., economic actors) is commonly modeled with respect to dependency and the number of actors involved: Dependency – in contrast to interdependency – means that there are many actors that depend on each other only via a single parameter.

The mechanism of interaction in this situation is typically a (perfect) market that connects actors only via the market price. With a decreasing number of actors the “degree of dependency” increases in terms of increasing interdependency. The extreme case of interdependency is a situation with only two actors, where outcomes entirely depend on each other’s behavior. With several or few (to two) actors involved, the mechanism of interaction is often modeled as a strategic game (e.g., as a bargaining game). Hence, the analytical continuum runs from markets (dependency) to strategic games (interdependency) with decreasing number of actors (see Figure 4).[61]

With respect to the number of actors learning may generally be affected in the following way: Starting from a situation with many actors, and all other things equal, with a gradual decrease in the number of actors the influence of the other actors’ behavior on each other increases, so that it becomes more important for a single actor to take the behavior of others into account (monotonistic increase in dependency).

Thus, more information has to be collected and processed by the actors as the behavior of single other actors becomes more relevant so that learning the other actors behavior becomes more important and difficult. However, at a certain number of actors there are so few actors (two at the margin) that learning becomes easier agin (see Figure 5). In Section 4.3., a separate hypothesis is added to capture this idea.

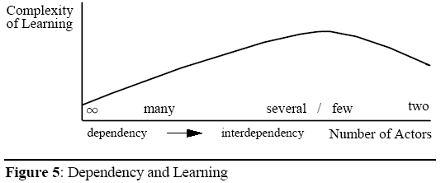
This line of reasoning implies, for example, that learning in perfect markets may be easiest, and may be most difficult in markets with several actors, while the difficulty of learning in twoperson markets may be between these two extremes.

However, as noted in the introduction to this section, in some situations this general pattern may be veiled by other structural factors, such as the availability of structural information, of knowledge, of correlating devices, of communication, and effects of collusion and reputation, so that learning (and the resulting behavior) may depend more upon these factors than on the number of involved actors. Therefore, it may not always be easy to isolate the effects of dependency on learning.

Uncertainty

Generally, and all other things equal, learning can be assumed to be more difficult under uncertainty than under certainty. Two types of uncertainty may affect learning: structural and strategic uncertainty. Structural uncertainty results when actors have incomplete information about the structure and know this. An interesting case of structural uncertainty is uncertainty about knowledge (i.e., actors don’t know what/if others know). Behavior is sensitive to this type of uncertainty and learning is likely to be more difficult under this condition.[62] From a purely theoretical point it is difficult to make predictions about differences in the effects of incomplete structural information versus structural uncertainty.

This may be mainly an empirical question. In Section 4.3 the hypothesis will simply be that uncertainty hinders learning. Strategic uncertainty arises if – with increasing dependency among actors – the behavior of other actors becomes more important so that strategic considerations play an increasing role. Therefore, learning to anticipate the behavior of others also becomes more important as the degree of dependency rises. That is, actors must form expectations about the behavior of others; often called beliefs. Strategic uncertainty refers to the extent to which agents’ beliefs differ, and is reduced by learning about actions of others and the observation of the outcomes of these actions.

Since this learning requires (inter)actions or at least information about the outcomes of (inter)actions, strategic uncertainty is a interaction determinant (see Table 1). However, because it requires feedback, as discussed in the next section, no separate hypothesis will be specified.

---

60 Of course, in tasks of individual decision making the number of actors is always one so that the following discussion does not apply to these tasks.

61 Note that perfect markets can be modeled as a n-person game in game theory, and that 2-person situations can be captured in traditional models. Thus, the degree of dependence does not imply a specific type of model, although there are clear advantages of each approach with respect to the number of actors.

62For an example of structural uncertainty in knowledge see ROTH & M URNIGHAN (1982) who found that the highest frequency of disagreement in a bargaining game of asymmetric occurred when only the player with the low price knew both prices, but was not sure if his opponent knew both prices (not common knowledge condition) because the player with the low price could not credibly signal that he had only a small price.

Prof. Tilman Slembeck

Next: Feedback

Summary: Index