Proof of Proposition 1

Substitute eqs. (3)-(4) and eq. (10) into eq. (12), and differentiate the resulting equation with respect to s, m and MA keeping p constant and noting that dm = ds = dp

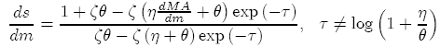(A1)

Since

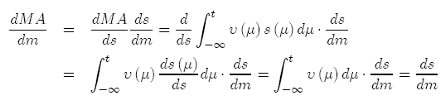(A2)

eq. (A.1) can be solved for ds/dm, and the proof is completed.

Proof of Proposition 2

By using integration by parts repeatedly,

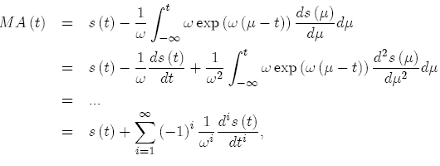(A3)

and the proof is completed.

Proof of Proposition 3

The dynamic system consisting of eqs. (1)-(5), eq. (9) and eq. (19) (assuming equality in the equation) can be written as a system of four first-order differential equations:

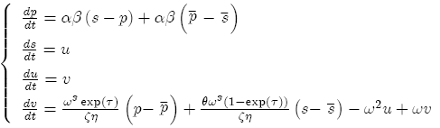(A4)

where we also have utilized eqs. (10)-(11). The Jacobian matrix evaluated at equilibrium i.e. dp/dt = ds/dt = du/dt = dv/dt = 0, is then

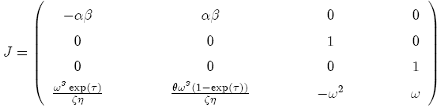(A5)

The dynamic system has four roots, which are denoted by λ₀, λ₁, λ₂ and λ₃. Then,

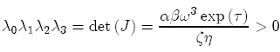(A6)

which means that zero, two or four roots has a negative real part. However, the case of four roots with a negative real part can be ruled out since the Routh-Hurwitz conditions are not fulfilled (Coppel, 1965, p. 158). Specifically, the Routh-Hurwitz conditions state that the necessary and sufficient conditions for a real polynomial of degree four,

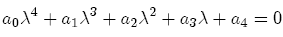(A7)

to have four roots with a negative real part are that

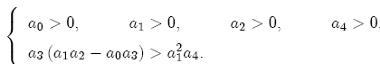(A8)

In this particular case, the characteristic equation, det (J - λl) = 0, is

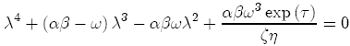(A9)

For example, a2 = -αβω 0. Then, let X_a,b,c be the 3 x 3 principal minor of J associated with the rows and columns a, b and c. Then, according to Theorem 1.2.12 in Horn and Johnson (1985, p. 42),

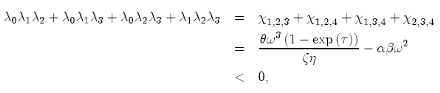(A10)

which rules out the case of zero roots with a negative real part. Therefore, two of the four roots have a negative real part, which means that the model is characterized by saddle-path stability and the proof is completed.

By Mikael Bask

Next: Books: Currency Market

Summary: Index