Long-run equilibrium

The equations that describe the money and the international asset markets, i.e., eqs. (3)-(4) can be solved to yield the price level in long-run equilibrium, if the aforementioned equality of the interest rates in long-run equilibrium is used:

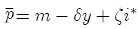(10)

Thus, the quantity theory of money holds in the long-run since dp/dm = 1. Furthermore, if we evaluate the equations that describe the goods market, i.e., eqs. (1)-(2), in long-run equilibrium and note that the price level is constant, i.e., dp/dt = 0, the exchange rate in long-run equilibrium can be solved to yield

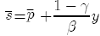(11)

Thus, the purchasing-power parity holds in the long-run since

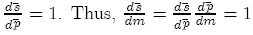
The overshooting phenomenon

Substitution of the expectations of chartists and fundamentalists, i.e., eq. (6) and eq. (9), into the expectations formation in eq. (5) yields

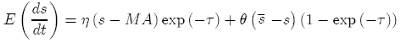(12)

Proposition 1 The impact effect of a monetary expansion is

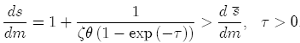(13)

Proof. See the Appendix for a proof.

In the immediate run, before goods prices have time to react, the exchange rate will rise more than the money supply and, thus, more than is necessary to bring the exchange rate to long-run equilibrium.

By letting τ-->∞, the expectations of portfolio managers coincide with the expectations of fundamentalists. Therefore, the equation describing the impact effect of a monetary expansion in Dornbusch (1976) is obtained:

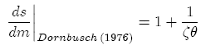(14)

Thus, the magnitude of exchange rate overshooting is larger in this model than in the Dornbusch (1976) model since

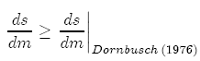(15)

and since ds/dm=1 in Dornbusch (1976). Moreover, according to Proposition 1, the extent of overshooting depends inversely on the planning horizon since

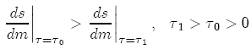(16)

By Mikael Bask

Next: Saddle-Path Stability

Summary: Index