The second step in resolving the question of whether the observed dynamics are chaotic or not, is taken by estimation of relevant statistical properties of the time evolution, i. e. so-called ergodic quantities. A basic virtue of the ergodic theory of dynamical systems is that it allows one to consider only the asymptotic properties of a dynamical system and thus neglect the transients' The focus, however, is on invariant probability measures rather than on attractors, which is the case within the geometric approach to dynamical systems.

With reference to the dynamical system in eq. (2.1) and the associated observer function in eq. (2.2), letting

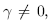
i. e. observational noise is present, an experimental time average of the observed time series may exist:

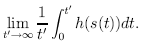
This time average in eq. (2.7) produces an invariant probability measure p on the attractor

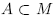
which describes how frequently various parts of A are visited by the trajectory, i.e. the time average of the observable h(s(t)) is equal to its space average p(h(s)). The probability measure p is invariant under the time evolution if

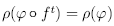
for every continuous function cp.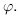

An invariant probability measure p is ergodic if it does not have a non-trivial
convex decomposition, i.e.

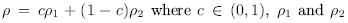
again invariant probability measures, and

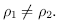
Because, in general, an invariant probability measure p can be uniquely represented as a superposition of ergodic measures, it is natural to assume p to be ergodic. If so, the ergodic theorem asserts that

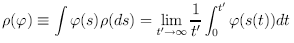
for every continuous function cp and for almost all initial conditions s(0) with respect to that measure p. This means that it makes sense to discuss the invariant statistical properties of the time evolution, i. e. ergodic quantities, like the Lyapunov exponents, the Kolmogorov (1958)-Sinai (1959) entropy and various definitions of the dimension of an attractor.

In general, however, it is exceptional that an attractor carries only one ergodic measure. For example, a so-called strange attractor, i.e. a chaotic attractor, typically carries uncountably many distinct ergodic measures. Normally, when observational noise is present in the observed time series, there is only one stationary measure p-y.' It may be the case that this so-called physical measure tends to a specific ergodic measure when -y - 0. Hereafter, however, it is assumed that any invariant probability measure carried by an attractor is ergodic.

The Lyapunov exponents for the dynamical system in eq. (2.1) with respect to the measure p measure the average exponential divergence or convergence of nearby but not equal initial conditions. Because the dynamical system is defined on an n-dimensional manifold, there are n Lyapunov exponents ranked from the largest to the smallest. A positive Lyapunov exponent measures the average exponential divergence of nearby initial conditions whereas a negative exponent measures the
average exponential convergence.

Thus, if we refer to the property of "sensitive dependence on initial conditions", a positive Lyapunov exponent is present when the dynamics are chaotic. The Kolmogorov (1958)-Sinai (1959) entropy of the measure p uses the fact that dynamical systems produce information and measures the average rate at which this information is produced. In the deterministic case, this means that the entropy of a non-chaotic dynamical system producing the measure p is zero because on average, only chaotic dynamical systems produce new information about the attractor generated
by the system.

In Pesin (1977), it is stated and proven that the Kolmogorov (1958)-Sinai (1959) entropy of a dynamical system is equal to the sum of the positive Lyapunov exponents whenever a physical measure p is present. As mentioned above, there are a number of definitions of the dimension of an attractor (Farmer et al., 1983). The dimension DA of a set, e.g. an attractor, is the amount of information needed to specify its points accurately, and is related to how hyper-volumes v scale as a function of a length parameter 1, i.e. V cc 1 D,1 .

For example, areas vary with the square of the length of the side and volumes vary with the cube. For fractal sets the dimension typically takes a non-integer value. The dimension of a dynamical system is important because it reveals the number of variables that are sufficient to mimic the systems behavior.

Prof. Mikael Bask

Next: Lyapunov exponents

Summary: Index