A. The Calculating Formula

Theorem If RL variable, X, follows Partial Distribution P( µ, σ²), then the optimal value of RL with its appearing probability is

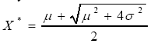(21)

where, µ is APL, and σ is the standard. The optimal value of RL with its appearing probability is optimal value of RL for short. Proof. According to expression (1), we denote

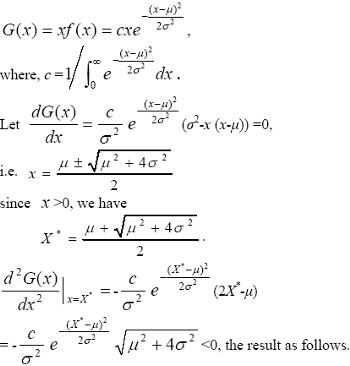
The expression (21) is the calculating formula for the optimal value of PL.

Corollary 1 If RL variable, X, follows Partial Distribution P( µ, σ²), and the optimal value of RL is given by (21), then the optimal margin between RL and µ is

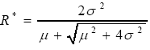(22)

Proof. According to formula (21), R*= X*- µ, the result as follows.

Corollary 2 If RL variable, X, follows Partial Distribution P( µ, σ²), and the optimal value of RL is given by (21), then the corresponding variance of RL , the actual risk, is 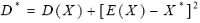(23)

Proof. According to expression (1) and (3),

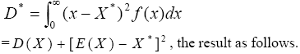
B. The examples

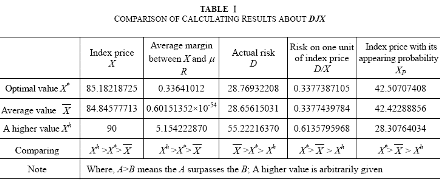
1) The optimal value of DJX and corresponding comparison analysis.

From the first example in VII, ˆ µ =84.84577713 and ˆσ ²=28.65615031.according to (2), (3), (21), (22) and (23), we have the calculating results shown in table I.

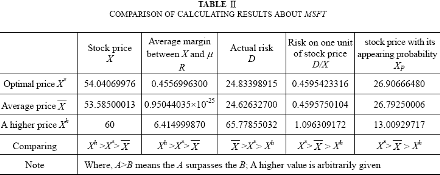
2) The optimal pricing of MSFT and corresponding comparison analysis. We take the close prices of MICROSOFT CP (MSFT) as sample data. Time: Jan. 29, 2002 -Dec. 24, 2002. By use of the method in [14],[15], the estimated values of parameters in partial distribution P( µ, σ²) are as follows:

ˆ µ =53.58500013; ˆσ ²=24.62632700.

According to (2), (3), (21), (22) and (23), we have the calculating results shown in table II.

We see, from table I and table II, that the average margin between X* and µ are higher than the average margin between X (E(X)) and µ, the risks on one unit of optimal value, X* , are lower than that of the average value of RL, and the optimal value X* with its appearing probability are higher than the average value X with its appearing probability. The later is important for director of an industrial enterprise or the fund manager to do their works. If we hope to have a higher value of RL, the risks on one unit of RL must be obviously higher, and the values with its appearing probability must be obviously lower.

Click to enlarge image

Click to enlarge image

Prof. Feng Dai, Prof. Song-tao Wu, Prof. Ya-jun Zhuang

Next: Conclusions and Remarks

Summary: Index