Implied Volatility (Smiles and Skews)

Now, if we know the value of the options, we can calculate the volatility for these instruments using the last explicit solution and a numerical method that solves {10} to converge to the unique implied volatility for this option price. (e.g. use the Newton-Raphson Method).

If we compute the implied volatility for market data using the option prices from table 1.1, we would expect the same volatility for all strikes and maturities for options with the same underlying price. However, it is well known that this is not what is observed.

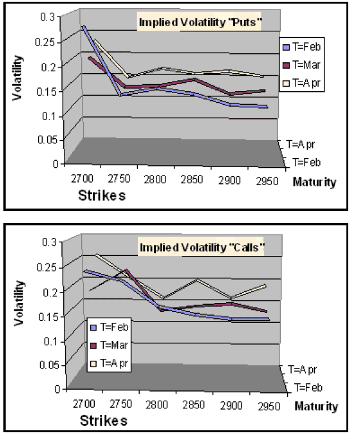
Figure 1.2.- Implied volatility of call and put options from table 1.1.

Most derivative markets exhibit persistent patterns of volatilities varying by strike. In some markets, those patterns form a smile curve. In others, such as equity index options markets, they form more of a skewed curve. This has motivated the name "volatility skew". In practice, either the term "volatility smile" or "volatility skew" (or simply skew) may be used to refer to the general phenomena of volatilities varying by strike.

Prof. Klaus Schmitz

Next: Local Volatility

Summary: Index