Given the prices of call or put options across all strikes and maturities, we may deduce the volatility which produces those prices via the full Black-Scholes- Merton equation. (Dupire, 1994 and Derman and Kani,1994)

• This function has come to be known as local volatility.

• Unlike the naive volatility produced by applying the Black-Scholes formula to market prices, the local volatility is the volatility implied by the market prices and the one factor BSM.

In 1994, Dupire [1] showed that if the spot price follows a risk-neutral random walk of the form:

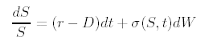
and if no-arbitrage market prices for European vanilla options are available for all strikes K and expiries T, then σL(K, T) can be extracted analytically from European option prices. If C(S, t,K, T) denotes the price of a European call with strike K and expiry T, we obtain the Dupire’s famous equation:

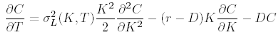
If we rearrange this equation we obtain the direct expression to calculate the local volatility (Dupire formula ):

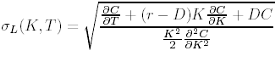
Problems using this equation

1.- One potential difficulty is that for strikes far in- or out-the-money the numerator and denominator of this equation may become very small, which could lead to numerical inaccuracies.

2.- Exchange traded options (market data) provide prices only at a limited, discrete set of strikes and maturities.

Suggested Solution:

If

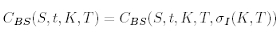
Where CBS(S, t,K, T, σI) is the Black-Scholes value for a European call with strike K, expiry T and implied volatility σI . Making this substitution for C(K, T) gives us an alternative expression for local volatility in terms of the derivative of the implied volatility (More information can be found in [2]).

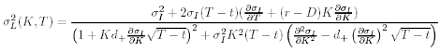
where

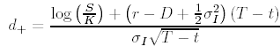
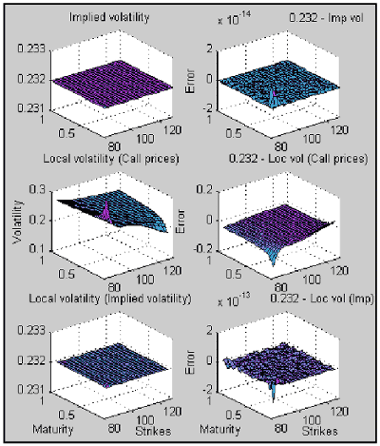
If we construct a huge matrix (MxN) = (300x200) with option prices using the Black-Scholes formula with a given volatility = 0.232, and we can calculate the local and implied volatilities, we see the following results (the error is the given volatility (0.232) less the calculated implied and local volatility).

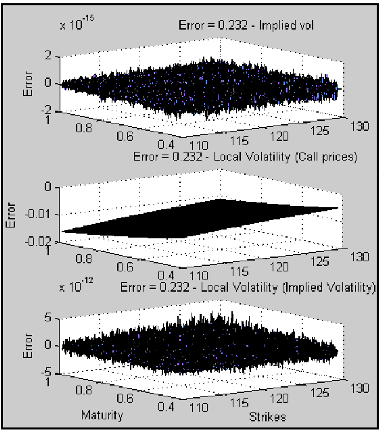
If we increase the time steps in the finite difference approximations (10 times), the option price is in the money, and the expiry is greater that 3 months, the local volatility as functions of call prices can give acceptable results. Otherwise we still obtain the results and behavior previewed below.

Important remarks about local volatility

1.- Calculating the local volatility with the implied volatility gives us a more accurate and stable result. Furthermore we can save huge amounts of computation time (30 times less).

2.- Using the last expression means that a flat implied volatility surface automatically yields a flat local volatility surface.

“Comments around the world”

“Implied volatility is the wrong number to put into wrong formula to obtain the correct price. Local volatility on the other hand has the distinct advantage of being logically consistent. It is a volatility function which produces, via the BSM equation, prices which agree with those of the exchange traded options”

Approximately Rebonato 1999

 

Prof. Klaus Schmitz

Next: Stochastic Volatility

Summary: Index