The aim with a stochastic volatility model is to incorporate the empirical observation that volatility appears not to be constant and indeed varies, at least in part, randomly. The idea is to make the volatility itself a stochastic process. Choices of models:
• Hull and White (1987)
• Heston (1993)
• ARCH
• GARCH
The phenomenon of the implied volatility smile shows that the Black-Scholes (1973) formula tends to systematically misprice out-of-the-money and in-themoney options if the volatility implied from the at-the-money option is used. Various stochastic volatility option pricing models (Hull and White 1987, Stein and Stein 1991, Heston 1993) have been developed to capture the “smile” effect. The most popular among them is the Heston Model because of its two main features: it allows the correlation between asset returns and volatility and it has a quasi-form pricing formula. The Heston option pricing formula is derived from the assumption that the stock price St and its return variance νt follow the risk-neutral random walk of the form:
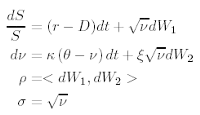
where κ is the mean-reverting speed, θ is the long-run mean, ξ is the volatility of volatility, dW1 and dW2 are two Wiener process (Brownian motion) with correlation coefficient, ρ. The four parameters κ, θ, ξ and ρ are assumed to be constant. The risk-free interest rate is also assumed to be constant.
The current price of a European call option with a strike price of K and a time to maturity of T is given by the following formula:
C(S, t,K, T) = S0P1 − Ke−rTP2
where, Pj , j=1,2, are two probability functions. The details of deriving the formula can be found in [3] or [7].
Problem # 1
The Heston Model uses the square root of the volatility in its equation, so if we use Monte Carlo with big ∆t to calculate the Heston option price, at some point, the model can give results as imaginary numbers.
Suggested Solutions:
1.- Use of the Milstein correction. if
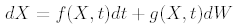
The solutions can be:
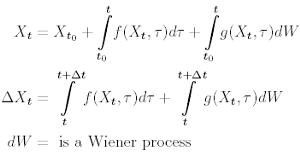
Possible approximations:
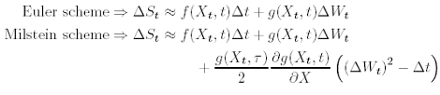so the Heston Model with Euler scheme has the form:
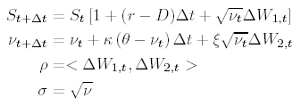
and the Heston Model with Milstein scheme has the form:
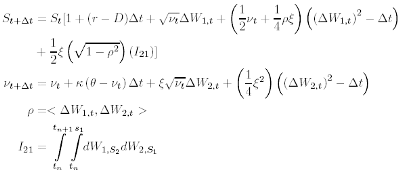
The details about how we can calculate the double integral or the derivation of the last equation, can be found in [7] or [5]. If we simulate both we can see that for a few cases (e.g. noise volatility of volatility) exit a big difference between them.
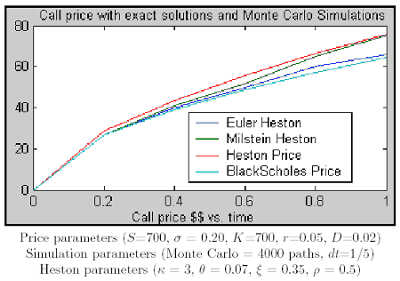
In conclusion, if we want to price exotics options with Heston volatility using Monte Carlo, Milstein scheme can give us the solution to a more accurate option price with less time computation. The Milstein correction term as well as the negative variance obtained in the Euler case marks the big difference between both schemes. More information and plots can be found in [7]
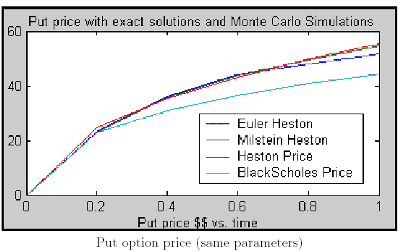
Problem # 2
How can we calibrate the Heston parameters to adapt the “Stochastic Heston Model” to the market data ?
Suggested Solutions:
1.- With the values of the option prices obtained from the market
error √ν = (Heston(κ, θ, ξ, ρ) market data)2
we can choose an optimization method to estimate the Heston parameters with the following conditions:
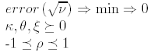
2.- Historical market data.
Note: Future Plans
Important remarks about Stochastic Volatility
1.- Stochastic Volatility models are useful because they explain why options with different strike K and maturity T have different Black-Scholes implied volatility and volatility smiles.
2.- The prices of exotic options given by models based on Black-Scholes assumptions can be wildly inaccurate, so dealers are motivated to find models which take the volatility smile into account when pricing exotic options.
3.- Pricing exotics options using Monte Carlo, Milstein scheme can give us the solution to a more accurate option price with less time computation. The Milstein correction term as well as the negative variance obtained in the Euler case marks the big difference between both schemes. More information can be found in [7]
Prof. Klaus Schmitz
Next: References
Summary: Index