Price returns (i.e. the di erence of two consecutive logarithmic prices) are widely investigated in finance, since their dynamics does not depend on size factors. For this reason we prefer to introduce a model for price dynamics that focuses its attention on logarithmic price, instead of price itself.
Let us consider the price S(t) of a financial object (an index, an exchange rate, a share quote) at time t, and define the logarithmic price as
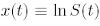
A moving average ¯x(t) based on logarithmic prices, that takes into account all the past with an exponentially time decaying weight, can be written in the form
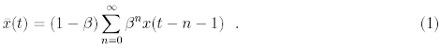
The moving average at time t is computed only with past quotes with respect to t, and x(t) is not included. This is not a relevant choice, since all the following could be reformulated in an equivalent way, including x(t) in the moving average.
The parameter 0 < β < 1 controls the memory length: for β = 0 we have the shortest (one step) memory ¯x(t) = x(t − 1), while when β approaches 1 the memory becomes infinity and flat (all the past prices have the same weight). More precisely, β determines the typical past time scale 1 − ln 2/ ln β up to that we have a significant contribution in the average (1).
Let us suppose that future price linearly depends on the di erence between the current price and the moving average, plus a certain degree of randomness. In our model x(t+1) is written as
x(t + 1) = x(t) + α[x(t) − ¯x(t)] + σω(t) (2)
where the ω(t) at varying t are a set of independent identically distributed random variables, with vanishing mean and unitary variance, so that σω(t) is a random variable of variance σ2. Indeed, our analysis focuses on the problem of correlations with moving averages and we expect that results would not qualitatively depend on the shape of ω distribution, which likely is a fat tails distribution [12–14].
The parameter −1 < α < +1 adjusts the impact of the di erence x(t) − ¯x(t) over the future price. Notice that a positive α means that the moving average is repulsive (the price most likely has a positive change if x(t) is larger then ¯x(t)), on the contrary the moving average is attractive if α is negative.
Also notice that the process loses all memory from the past for α = 0, independently on β, becoming a pure random walk. Let us stress that the Vasicek model [15] is a particular case in our more general scheme, corresponding to the peculiar choice β = 1.
According to (2), the return r(t), defined as
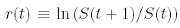
turns out to be r(t) = α[x(t)− ¯x(t)]+σω(t). Let us stress that the first contribution is measurable at time t just before the price change and, therefore, is an available information for the trader. It is easy to check that the moving average (1) satisfies
¯x(t + 1) = (1 − β)x(t) + β¯x(t) .(3)
Equations (2) and (3) define a two-component linear Markov process. Such a process can be solved by a diagonalization procedure. After having defined
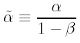
and
ε ≡ α + β
which must satisfy −1 < ε< 1, we introduce a new couple of variables, linear combinations of x(t) and ¯x(t)

being y(t) simply the di erence between the logarithmic price and its moving average at time t. The system turns out to be diagonal in terms of the new variables
y(t + 1) = εy(t) + σω(t) z(t + 1) = z(t) + σω(t) ,
and therefore can be easily solved, obtaining
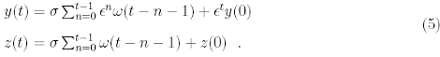
The steady distribution p˜σ(y) of y can be derived from equation (5), once given the ω. The variance of y, ˜σ2, can be directly computed
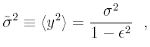
where <.> means average over the ω distribution.
The solution in terms of x(t) and ¯x(t) can be obtained from (5) by using the inverse transformation of (4).
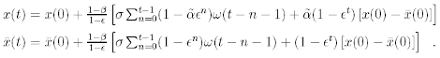
By Prof. R. Baviera, Prof. M. Pasquini, Prof. J. Raboanary and Prof. M. Serva
Next: Data Analysis
Summary: Index