It is widely believed that the celebrated Black-Scholes model [4] cannot describe option prices dynamics in real markets. The characteristic observed effects of “smiles” and “skews” contrast with the assumption of constant volatility of the underlying asset. Indeed there is strong evidence that volatility depends in some way on the present stock price (leverage effect) and on past prices realization (volatility persistence), as well as on the moneyness, time and maturity (volatility term structure): we refer, for instance, to Tompkins [24], Derman and Kani [8], Ghysels, Harvey and Renault [13], Bollerslev, Chou and Kroner [5]. For this reason many authors have developed variations of the Black-Scholes model, aiming to capture at least some of the above observed features.

Within the framework of continuous Itˆo processes, these alternative theories divide in two broad classes: single-factor models in which the volatility is a deterministic function of present or past values of the underlying price, and multifactor models that allow for exogenous stochastic influence (see, for instance, the monograph by Epps [11] and the recent papers by Barucci, Malliavin, Mancino, Ren`o and Thalmaier [2], Davis [7] for comprehensive bibliographic references). An apparent advantage of single on multi-factor models is that the Brownian motion which drives the asset price is the only source of randomness. Then the arbitrage argument that underlies the Black-Scholes model is preserved and there are unique preference-independent prices for contingent claims. The simplest single-factor model is the so-called level dependent volatility in which the underlying price St satisfies

where B ia a Brownian motion and s = s (t; St) is a deterministic function of the current value St and time. Special cases are the CEV model by Cox and Ross [6] where

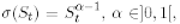
and the implied tree models by Derman and Kani [8], Dupire [10] and Rubinstein [23].

Empirical analysis has shown that level dependent volatility still fails to price derivative securities better than does the usual Black-Scholes model. This is the conclusion of the study by Dumas, Fleming and Whaley [9] who suggest a volatility related to past changes of the underlying prices, as the last candidate model before resorting to fully stochastic volatility. An interesting class of such models was proposed by Hobson and Rogers. In [14] a specific version is examined in which the volatility is defined in terms of the difference between the current price and an exponential average of past prices. As in the discrete-time ARCH and GARCH environments, this is designed to reflect the perception that large movements of the asset price in the past tend to forecast higher future volatility.

In [14] it is shown that the model exhibits indeed a wide variety of smiles and skews, and can account for volatility term structures as the average of prices evolves through time (see also the study by Fig`a-Talamanca and Guerra [12]). Hobson and Rogers claim to solve numerically the associated PDE by a finite-difference method: unfortunately no scheme is explicitly given in [14], nor convergence results are proved. Actually, these results can be hardly obtained by the “classical” theory of parabolic PDEs. Indeed, incorporating past prices enters an additional state variable on which the derivative’s arbitrage-free price depends. Then, as in the case of path-dependent contingent claims such as Asian or look-back options, the augmented PDE associated to the model is strongly degenerate and standard analytical and numerical techniques do not apply.

On the other hand, we recall that Barucci, Polidoro and Vespri [3] successfully studied the problem of pricing Asian options in the framework of PDEs of Kolmogorov type. This class of degenerate diffusion PDEs, whose precise definition is given in Section 2, shares most of the prominent features of classical parabolic equations. In this note we present analytical and numerical results on Kolmogorov PDEs with variable coe±cients which apply to the Hobson-Rogers model for European and Asian-style derivatives. Consequently we wish to emphasize the mathematical tractability of this model. Indeed our results are comparable with the known ones for the classical Black-Scholes environment.

In particular, we aim to propose a finite-difference scheme for the Hobson-Rogers model and prove convergence results. Let us recall that nonlinear Kolmogorov equations have also been recently considered for pricing options with memory feedback by Peszek [21] and for a stochastic differential utility problem by Antonelli and Pascucci [1], Pascucci and Polidoro [20]. The note is organized as follows. In the next section, we present theoretical results about Kolmogorov PDEs which allow to treat a variety of path-dependent contingent claims. In Section 3, we prove numerical results by suitably adapting finite-differences schemes to the degenerate setting.

M. Di Francesco, A. Pascucci www.dm.unibo.it/~pascucci

Next: Kolmogorov equations

Summary: Index