¯¯¯ We are concerned with the numerical solution to the Cauchy problem for the KE (2.4). Here we extend some results by Barucci, Polidoro and Vespri [3] for the homogeneous KE (2.2) with constant coe±cients. As we shall see below, the main new di±culties in treating the Hobson-Rogers equation (2.4) are due to the lack of homogeneity. Our scheme allows to consider the problem

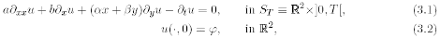
where a = a(x, y, t) = a0 > 0 and a , ß e R, a ? 0.

Preferring straightforwardness to generality, we assume that the coe±cients a; b are smooth functions with bounded derivatives. We remark explicitly that condition a ? 0 ensures that (3.1) is a KE since it verifies the Hormander condition. To fix the ideas, we first consider the case of the model equation 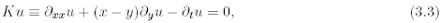correspondent to a = a = 1 = - ß and b = 0 in (3.1). In view of the theory of KEs, it seems natural to consider and approximate the first order operators related to the equation as in (2.9), rather than the Euclidean derivatives as usual. Thus, as in Example 2.3, we consider, for fixed x, y, the first order part of K as a unique “directional” derivative which we denote by Y :

We aim to approximate operator K by finite differences on the uniform grid

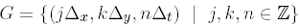
Since K is strongly degenerate, it is known that the classical parabolic boundary value problem for (3.3) is not well posed. In order to comply with the non Euclidean geometry naturally to associated to K, we impose

Since equation (3.3) is not homogeneous (in the sense of (2.14)), then the discrete operator that one might naively associate to K is not well defined on G because it involves points not belonging to the grid. However it is possible to approximate K e±ciently by the following “corrected” operator

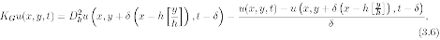
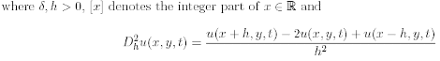
is the usual second order central di®erence. Indeed we have:

Lemma 3.1 Operator KG is well defined on the grid G with

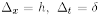
and approximates K in the sense that

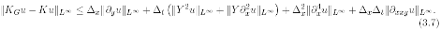
Proof. By (3.5), the first assertion is obvious. To prove (3.7), we first observe that

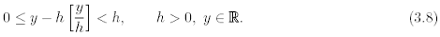
Then we have

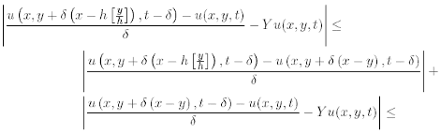
(by the mean value theorem and (3.8))

An analogous estimate for the second order part of K completes the proof.

Lemma 3.2 [Maximum principle] Let v be a solution to the discrete Cauchy problem

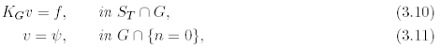
where f, ? are bounded functions. If the following stability condition holds

then

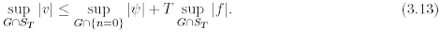
Proof. Let us denote

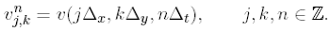
Once we have observed that (3.10) is equivalent to

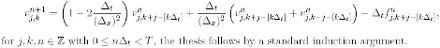
Lemma 3.3 If f is Lipschitz continuous in R^N and u is a solution to problem (2.17), then for every s e ]0, T[ we have

where the constant c only depends on K; T and the Lipschitz constant of f.

Proof. By the representation formula (2.16) it suffices to consider the case t = 0. Then, if C = C(t) denotes the matrix in (2.12) with A = µ Ip, by (2.16) and (2.18) we infer

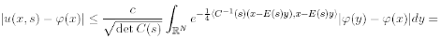
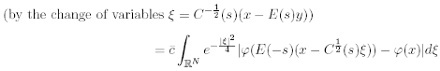
and the thesis follows by the Lipschitz continuity of f:

We are now in position to prove the following convergence result.

Theorem 3.4 Let u be a solution to the Cauchy problem (3.3)-(3.2) with initial datum f bounded and Lipschitz continuous. Let uG be a solution to the correspondent discrete problem (3.10)-(3.11) with f = 0 and ? = f. Assume the stability condition (3.12). Then uG tends to u uniformly on compacts.

Proof. Fixed a suitably small s > 0, we define

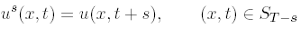
and we denote by u ^s G the solution to (3.10)-(3.11) with f = 0 and ? = u ^s(., 0). Let M be a compact subset of R²]x0, T[. By Lemma 3.3, we have

Moreover, keeping in mind that

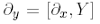
is a third order derivative, by the representation formula (2.16) and estimate (2.18), we have

with c independent on s. Now, the function 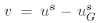is a solution to (3.10)-(3.11) with 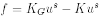and initial datum ? = 0. Therefore, applying to v the maximum principle and Lemma 3.1 combined with the estimates (3.16) and the stability condition (3.12), we get

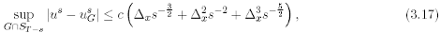
with c = c(f).

Finally, us u is a solution to (3.10)-(3.11) with f = 0 and initial datum ? = u( ., s)- f. By (3.15),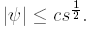

Hence, by the maximum principle, we haveCombining (3.15), (3.17) and (3.18), we deduce

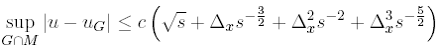
and, by choosing 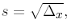we get

where the positive constant c only depends on K;M and f.

Remark 3.5 The rate of convergence of the scheme is explicitly given in (3.19). Clearly it is not comparable with the classical results for parabolic PDEs and it is consequent to the correction operated in the definition of KG in (3.6). As a refinement of the above scheme, one can use linear interpolation and approximate K by the discrete operator

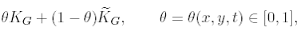
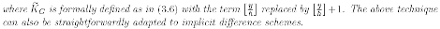
Theorem 3.4 can be straightforwardly generalized to problem (3.1)-(3.2). In the definition of the grid, (3.5) should be replaced by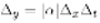

and the approximating operator becomes

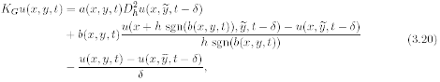
where

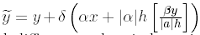
In (3.20), the first order term bux is approximated by the usual upwind difference, that is by using the forward difference where b is positive and the backward difference where it is negative. Then we have

Theorem 3.6 Let u be a solution to (3.1)-(3.2) and uG a solution to (3.10)-(3.11) with f = 0 and ? = f. Under the stability condition

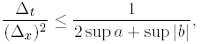
for every compact subset M of R² x]0, T[ there exists a positive constant c such that

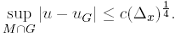
M. Di Francesco, A. Pascucci www.dm.unibo.it/~pascucci

Next: Reference

Summary: Index