Appendix 1: The Double Poisson Distribution
The double Poisson distribution, for the integer valued positive random variable y, has the following expression:
Where c(µ, φ) is a constant (with respect to y) such that the probabilities add to one. Efron
(1986) shows that the value of c(µ, φ) varies little with respect to µ and φ . He also provides
the approximation 
and he suggests maximising the approximate
likelihood (leaving out the highly nonlinear multiplicative constant) in order to estimate the
parameters and using the correction factor when making probability statements using the
density.
Appendix 2: Copulas
Copulas provide a very general way of introducing dependence among several series with
known marginals. Copula theory goes back to the work of Sklar (1959), who showed that
a joint distribution can be decomposed into its K marginal distributions and a copula, that
describes the dependence between the variables. This theorem provides an easy way to form
valid multivariate distributions from known marginals. A more detailed account of copulas
can be found in Joe (1997) and in Nelsen (1999). Let H(y1,..., yK) be a continuous K-
variate cumulative distribution function with univariate margins Fi (yi), i = 1,...,K, where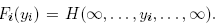 
According to Sklar (1959), there exists a function C, called
copula, mapping [0, 1]K into [0; 1], such that:
The joint density function is given by the product of the marginals and the copula density:
while there are many alternative formulations for copulas in the bivariate case, the number of possibilities for multi-parameter multivariate copulas is rather limited. We choose to work with the most intuitive one, which is arguably the Gaussian copula, obtained by the inversion method (based on Sklar, 1959). This is a K-dimensional copula such that:
and its density is given by,
where ΦK is the K-dimensional standard normal multivariate distribution function,Φ-1 is the inverse of the standard univariate normal distribution function and q = (q1,..., qK)' with normal scores qi = Φ-1 (zi), i = 1,..., K . Furthermore, it can be seen that if Y1,...., YK are mutually independent, the matrix Σ is equal to the identity matrix IK and the copula density is then equal to 1.The joint density of the counts in the Double Poisson case with the Gaussian copula is:
denotes the Double Poisson density as a function of the observation N i,t the conditional mean µ*i,t and the dispersion parameter φi . c denotes the copula density of a
multivariate normal and θ = (ω, vec(A), vec(B)). The q i,t gathered in the vector qt are the
normal quantiles of the z i,t :
where the z i,t are the PIT of the continuoused count data, under the marginal densities (see Appendix 3 for details). Taking logs, one gets:
We consider a two-stage estimator as in Patton (2002). Given that we use the multivariate normal copula, the second step of the two-stage procedure does not require any optimisation, as the MLE of the variance-covariance matrix of a multivariate normal with a zero mean, is simply the sample counterpart:
It is important to realise that correct specification of the density in the marginal models is crucial to the specification of the copula, as any mistake would have as a consequence the fact that the uniformity assumption is violated, which would invalidate the use of copulas.
Appendix 3: Discrete Distributions and PITT
The problem with discrete distributions is that the probability integral transformation theorem (PITT) of Fisher (1932) does not apply, and the uniformity assumption does not hold, regardless of the quality of the specification of the marginal model. The PITT states that if Y is a continuous variable, with cumulative distribution F, then
Z = F(Y )
is uniformly distributed on [0; 1]. Denuit and Lambert (2002) use a continuousation argument to overcome these difficulties and apply copulas with discrete marginals. The main idea of continuousation is to create a new random variable Y* by adding to a discrete variable Y a continuous variable U valued in [0; 1], independent of Y , with a strictly increasing cdf, sharing no parameter with the distribution of Y , such as the uniform on [0; 1] for instance:
Y* = Y + (U - 1) ,
As can be seen, knowing the value of Y* , which is the new continuous variable, is equivalent to knowing the value of the underlying count. If Y* = 4:38275629, then we know that Y = 5. Hence we do not lose any information by creating this new variable. Using continuousation, Denuit and Lambert (2002) state a discrete analog of the PITT. If Y is a discrete random variable with domain χ, in N, such that fy = P(Y = y), y ε χ, continuoused by U, then
is uniformly distributed on [0, 1], and [Y ] denotes the integer part of Y . In this paper, we use the continuoused version of the probability integral transformation in order to test the correct specification of the marginal models. If the marginal models are well-specified, then Z*, the PIT of the series under the estimated distribution and after continuousation, is uniformly distributed.
By Dr W. B. Omrane and A. Heinen
Next: Table
Summary: Index