Choose

and

such that

for some

where

is the fixed point of T_p on

and c is the contractivity constant of T_p. Moreover, the function

is convex.

Thus, the following constrained optimization problem:

(P)

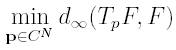
can always be solved at least numerically. Another way of choosing the form of T_p is the direct approach, that is the following. Choose n = N +1 points on [0, 1], (x₁, . . . , x_n), and assume that 0 = x₁ < x₂ < · · · < x _n−1< x_n = 1. The proposed functional is the following

open full size image

i = 1, . . . , n−1, where u is any member in the space

Notice that T_F is a particular case of T_p where

and

This is a contraction and, at each iteration, T_F passes exactly through the points F(x_i). It is almost evident that, when n increases the fixed point of the above functional will be "close" to F. For n small, the choice of a good grid of point is critical. So one question arises: how to choose the n points ? One can proceed case by case but as F is a distribution function one can use its properties. We propose the following solution: take n points (u₁ = 0, u₂, . . . , u_n = 1) equally spaced [0, 1] and define q _i = F^-1, i = 1, . . . , n. The points q _i are just the quantiles of F. In this way, it is assured that the profile of F is followed as smooth as possible. In fact, if two quantiles qi and q _i+1 are relatively distant each other, than F is slowly increasing in the interval (q _i, q _i+1) and viceversa. This method is more efficient than simply taking equally spaced points on [0, 1]. With this assumption the functional T_F reads as

open full size image

This form of the estimator proposes an intuitive (possibily) good candidate for distribution function estimation. Note that we overcome the problem of moment matching as we don't even need the existence of the moments.

Stefano M. Iacus, Davide La Torre

Next: Corollary 6.

Summary: Index