In Matlab un polinomio è rappresentato da un vettore. Per creare un polinomio è sufficiente immettere i coefficiente del polinomio in un vettore in ordine decrescente. Per esempio, consideriamo il seguente polinomio:
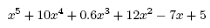 (3.1)
(3.1)
Per inserirlo nel Matlab, è sufficiente registrarlo come un vettore nel modo seguente:
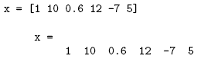
Il Matlab può interpretare un vettore di lunghezza n+1 come un polinomio di ordine n. Per i coefficienti non presenti nel polinomio si deve inserire lo zero nella corrispondente posizione del vettore. Per esempio,
x5 - 7x + 5 (3.2)
in Matlab deve essere rappresentato come:
y = [1 0 0 0 -7 5]
Si può calcolare il valore del polinomio usando la funzione polyval. Per esempio, per trovare il valore del precedente polinomio per s=2,
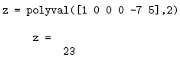
E’ anche possibile estrarre le radici di un polinomio. Ciò è utile quando si ha un ordine elevato del polinomio, come
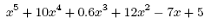 (3.3)
(3.3)
Per trovare le radici basta semplicemente inserire il seguente comando:
roots([1 10 0.6 12 -7 5])
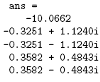
La moltiplicazione tra due polinomi è data dalla convoluzione dei loro coefficienti. La funzione usata dal Matlab è conv.
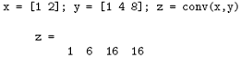
La divisione di due polinomi viene realizzata con la funzione deconv che restituisce il resto e il risultato. Dividere z per y equivale ad ottenere x, secondo quanto fatto sopra:
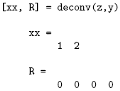
Come si può vedere, questo è il polinomio x cercato. Se z non fosse un multiplo di y, il vettore del resto avrebbe alcuni elementi diversi da zero. Per sommare due polinomi dello stesso ordine, come già visto, basta eseguire z=x+y (i due vettori devono avere la stessa lunghezza). Nel caso generale,e cioè quando i due polinomi sono di grado diverso, puoi usare la funzione da definire, polyadd.

Per usare polyadd, copia la funzione in un m-file, così da poterla utilizzare come una qualsiasi funzione del toolbox del Matlab. Assumendo che la funzione sia stata creata, il comando è copletato aggiungendo i polinomi x e y (osserva che in questo esempio i polinomi hanno grado diverso):
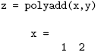
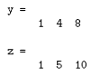
G. Ciaburro
Successivo: Risoluzione di sistemi di equazioni lineari
Sommario: Index