Sulla base di quanto definito nel paragrafo precedente, è possibile formulare una procedura per la stima del numero dei
neuroni dello strato intermedio.
Definizione 2 Sia (  ) d la probabilità che
) d la probabilità che
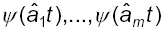
siano linearmente indipendenti  , fissato n e m, tenendo conto della costante d>0 definita nel paragrafo precedente. Sia
, fissato n e m, tenendo conto della costante d>0 definita nel paragrafo precedente. Sia

dove #B d è il numero delle volte che
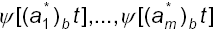
sono linearmente indipendenti tenendo conto della precisione del calcolo numerico (d).
Dato che d non dipende da n, m, f(.) e s2 allora
 (5) uniformemente.
(5) uniformemente.
Fissata una costante ? d >0, che dipende solo da d, si possono ipotizzare i seguenti casi:

e dove :
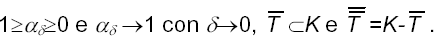
Dato n 0 e m, 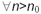 si può costruire un test per verificare l'ipotesi che
si può costruire un test per verificare l'ipotesi che
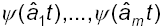
siano linearmente indipendenti  Sia a l'errore di I specie e ? a il relativo percentile della Normale
Sia a l'errore di I specie e ? a il relativo percentile della Normale
standardizzata, allora si ha 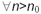 si può costruire un test per verificare l'ipotesi che
si può costruire un test per verificare l'ipotesi che
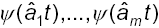
siano linearmente indipendenti  Sia a l'errore di I specie e ?a il relativo percentile della Normale standardizzata, allora si ha
Sia a l'errore di I specie e ?a il relativo percentile della Normale standardizzata, allora si ha
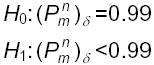
Considerando un n sufficientemente grande si ha la statistica test: Quindi si accetta l'ipotesi nulla se ? m > ? a .
Procedura proposta (dimensione della base)
1. Si parte da m=2.
2. Si costruisce la statistica test ?m.
3. Se ? m > ? a allora la base è maggiore di m; si incrementa m e si
ritorna al passo 2. Altrimenti la base è m-1.
Quindi si ha una batteria di test
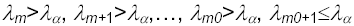
da cui la dimensione della base è m 0 .Tale procedura è consistente se
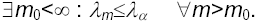
La procedura indicata consente di stimare il numero minimo di neuroni dello strato intermedio tale da garantire un MISE = d.
Successivo: Risultati Empirici
Sommario: Index