Per analizzare la performance della procedura indicata nel paragrafo precedente è necessario considerare gli elementi che influenzano la stima:
. n il numero di osservazioni;
. f(.) la funzione incognita che descrive il Trend;
. s 2 la varianza del WN nel modello (1).
Ricordando che lo stimatore rete neurale è uno stimatore globale rispetto al criterio dell'errore quadratico medio, allora è facile vedere che:
. se s 2 ? 0 
la stima tende a f(t), per n ?8;
. se s 2 ? 8 la stima tende ad una costante, f(t)=c 
.
Quindi l'esperimento di simulazione è stato fatto considerando due diverse forme funzionali per f(.) e due diversi valori per n, il numero di osservazioni della serie storica. Sia
. f (1) (t) = 4.26(exp(-t)-4exp(-2t)+3exp(-3t)) la funzione di wahba ;
. f (2) (t) = 0
. n 1 =100;
. n 2 =300.
La variabile indipendente t è definita come una sequenza uniforme di lunghezza n i , i=1,2, nel compatto [0.1 , 0.4]. La e t del modello (1) si distribuisce come una Normale. Quando si considera f (1) (t), s 2 è fissata al 20% della varianza dello stesso segnale f (1) (t). Nel caso di f (2) (t), s 2 è posta a 0.2.
del modello (1) si distribuisce come una Normale. Quando si considera f(1)(t), s2 è fissata al 20% della varianza
dello stesso segnale f(1)(t). Nel caso di f(2)(t), s2 è posta a 0.2. Quindi si avranno quattro serie simulate:
.Y t (1) = f (1) (t)+e t , t=1,...,n 1 ;
.Y t (2) = f (2) (t)+e t , t=1,...,n 2 ;
.Y t (3) = f (3) (t)+e t , t=1,...,n 3 ;
.Y t (4) = f (4) (t)+e t , t=1,...,n 4 ;
Le serie Y t (i) , i=1,2,3,4, sono scalate in [0.1 , 0.9]. La simulazione è stata fatta con 100 repliche Monte Carlo. Nella stima di ( 
) s si è considerata una q pari a 30.
Grafico 1: n 2 osservazioni, Y t (2) è la serie simulata, la stima neurale del Trend con m=4 neuroni applicando la procedura proposta.
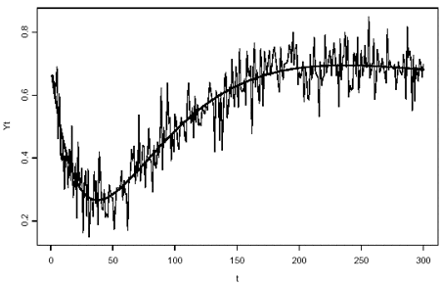
Il grafico 1 mostra un esempio della procedura proposta applicata ad una serie simulata Y t (2) , da cui si stima un valore di m pari a 4. Invece il grafico 2 mostra una serie simulata Y t (4) da cui si ottiene un m pari a 3 per la stima neurale. Questo esempio mette in evidenza come una forma funzionale relativamente più semplice (grafico 2) è stimata bene già con 3 neuroni nello strato intermedio mentre l'altro caso (grafico 1) presenta una forma funzionale per il Trend più complessa per la quale bastano 4 neuroni.
Grafico 2: n 2 osservazioni, Y t (4) è la serie simulata, la stima neurale del Trend con m=3 neuroni applicando la procedura proposta.
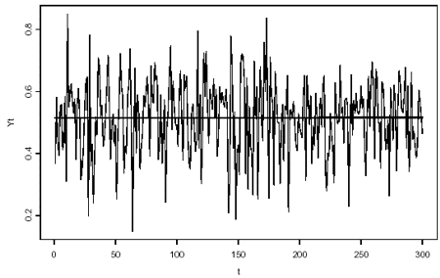
Tabella 1: Distribuzione delle 100 repliche Monte Carlo rispetto al numero dei neuroni stimati (m) relativamente alla
funzione Wahba, per i due casi Y t (1) e Y t (2) .
Tabella 2: Distribuzione delle 100 repliche Monte Carlo rispetto al numero dei neuroni stimati (m) relativamente alla
funzione costante, per i due casi Y t (3) e Y t (4) .
Sia la tabella 1 che la 2 mostrano che all'aumentare del numerosità n, la stima di m tende a diminuire poiché a parità di errore del MISE, diminuisce la variabilità degli stimatori e quindi deve diminuire anche m (vedi paragrafo 3, Giordano e Perna). Invece, a parità di numerosità n, la stima di m è legata alla "roughness" della funzione f(t). Infatti la funzione di Wahba presenta dei punti di pendenza relativamente accentuati rispetto al caso di una funzione identicamente costante. Quindi la funzione di Wahba è sicuramente più "roughness" della funzione identicamente costante e di conseguenza la stima di m aumenta al crescere della "roughness" nella funzione stessa.
Successivo: Conclusioni e sviluppi futuri
Sommario: Index