Lo sviluppo della geometria dei frattali è stato uno dei progressi più importanti ed affascinanti che la matematica ha avuto in questo secolo. Con i frattali i matematici hanno creato un sistema che descrive le forme naturali in termini di poche e semplici regole. I frattali danno struttura alla complessità e bellezza al caos.

La visione del mondo della geometria dei frattali è totalmente diversa da quella della geometria Euclidea.

Euclide ha ridotto la natura in oggetti semplici e simmetrici: il punto, la linea ad una dimensione, il piano a due dimensioni ed il solido tridimensionale.
In realtà, se osserviamo la natura, vediamo che essa rifiuta la simmetria e che non esistono in natura linee, piani e solidi perfetti così come descritti dalla geometria Euclidea; le montagne non sono coni e le nuvole non sono sfere
Benoit Mandelbrot può essere considerato l'Euclide della geometria dei frattali. Egli ha combinato il suo punto di vista e le sue osservazioni con quelle di altri matematici dando vita ad una geometria della natura profondamente diversa da quella tradizionale.

Forse il fallimento della geometria classica nel descrivere gli oggetti naturali è ben descritto dalla seguente proprietà. Per quest'ultima un oggetto diventa sempre più semplice via via che si guarda in modo più approfondito. Un solido tridimensionale diventa un piano bidimensionale, poi una linea fino ad arrivare al punto.

Un oggetto naturale dimostra invece di avere tanti più dettagli quanto più approfonditamente si guarda. Gli oggetti frattali godono della stessa proprietà: più da vicino vengono esaminati, più dettagli possono essere visti. A questo punto ci si chiede cosa sia precisamente un oggetto frattale. La parola frattale deriva dall'aggettivo latino "fractus" che significa interrotto o irregolare.
Un frattale è un oggetto di forma estremamente irregolare o estremamente interrotta e frammentata e che rimane tale qualunque sia la scala alla quale lo si esamina.

Quest'ultima proprietà si chiama "autosomiglianza": a qualunque scala si osservi, il frattale presenta sempre gli stessi caratteri globali. Ciò significa che le varie parti hanno una qualche relazione con l'intera forma dell'oggetto. Per fare un esempio di oggetto frattale possiamo pensare ad un albero. Ogni ramo, con i suoi rami ancora più piccoli che da esso si diramano, è, in un senso qualitativo, simile all'intero albero.

Abbiamo appena visto cos'è un oggetto frattale. Ci chiediamo adesso se tale concetto può essere esteso anche alle serie storiche, ovvero se una serie storica può esibire caratteristiche simili a quelle di un oggetto frattale. Per una serie storica tutto ciò significa possedere la proprietà di "autosomiglianza statistica" rispetto al tempo cioè, qualunque sia l'intervallo temporale delle osservazioni, la serie dimostra di avere sempre caratteristiche statistiche simili.

Guardiamo ad esempio le figure che seguono:

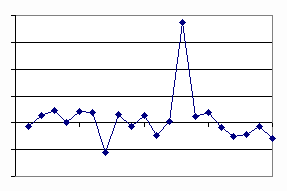
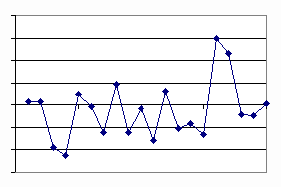
Esse rappresentano i rendimenti giornalieri, settimanali e mensili dell'indice COMIT della borsa italiana per venti osservazioni successive. Senza indicazioni sugli assi cartesiani non si riesce a distinguere ad esempio il grafico dei rendimenti giornalieri da quello dei rendimenti mensili, quello dei rendimenti settimanali da quello dei rendimenti mensili e così via.

Questi grafici mettono visivamente in evidenza la proprietà di autosomiglianza in una serie storica. Nel prossimo paragrafo vedremo come è possibile stabilire se una serie storica segue un random walk o se invece il suo andamento rispecchia la presenza di una sottostante struttura frattale nel senso che abbiamo appena visto.

Alessandro Caforio

Successivo: L'esponente "H" di Hurst

Sommario: Indice