Quando si utilizzano tecniche non parametriche per modellare i dati vengono formulati molti modelli. È importante, quindi, prendere in considerazione alcune misure per poter ordinare i modelli in base alla loro bontà nella fase di ricerca e per poter scegliere il miglior modello nella fase finale. Un criterio molto utilizzato è la Variance Reduction (VR):
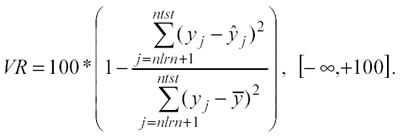
VR è una buona misura di performance per valutare differenti modelli e per distinguere i buoni predictors dai cattivi. Se 0 = VR significa che il modello condurrà a previsioni pari alla media dei valori osservati, se 0 < VR l’informazione previsionale è inferiore alla semplice media, mentre, se 0 > VR significa che il modello conduce a previsioni migliori che non la semplice media e dunque è un modello da considerare.
VR è una quantità priva di dimensione che non dipende dalla dimensionalità della variabile y, pertanto può essere ritenuto un buon indice di confronto anche tra modelli di natura diversa. Il problema principale nell’uso di VR è che soffre la presenza degli outliers: se esistono anche solo pochi punti di y, che sono molto lontani dalla superficie del modello yˆ , questi tenderanno ad avere un effetto sproporzionato sulla valutazione della bontà del modello.
Per ridurre l’effetto degli outliers, nella valutazione del modello è bene usare altri indicatori congiuntamente a VR, per esempio: − La Median Variance Reduction (MVR), definita come segue:
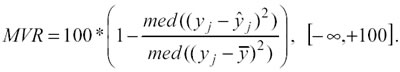
dove med è l’operatore mediana. Questo indicatore offre una valida risposta al problema degli outliers, ma aggiunge complessità computazionale al processo, data dalla presenza dell’operatore mediana.
Il Fraction Same Sign (FSS) misura la frazione di punti predetti ( j ) il cui segno (+,–) coincide con i valori osservati (yj) sotto l’ipotesi
che e y abbiano media pari a zero, in formula si ha:
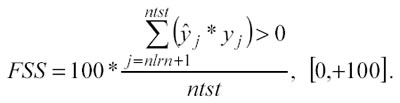
FSS può essere un buon indicatore poiché, se il modello riesce a predire il segno di yj , si possono sviluppare efficaci strategie di trading, in ogni caso non è una misura da sopravvalutare e va usata congiuntamente ad altri indicatori. Il problema nell’uso di FSS sta nel fatto che i valori di j e yj vicini allo zero vengono trattati allo stesso modo dei valori molto diversi da zero; ciò nonostante, data la facilità di calcolo, è bene usare FSS come parametro di output in tutti i report finali.
Il coefficiente di determinazione al quadrato
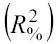
indica la capacità esplicativa del modello:
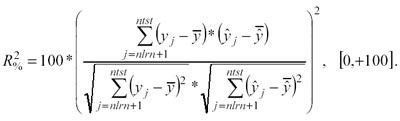
Quando si modellano i mercati finanziari per fare trading è indispensabile analizzare la performance dei trades generati dal trading system basato sul modello da verificare. Invece di misurare quanto j yˆ si discosta da yj, con questo criterio si va ad analizzare direttamente i rendimenti. È superfluo considerare questo approccio nella fase di ricerca del modello (selezione dei best predictors), ma è d’obbligo nella valutazione dei modelli finali sull’evaluation set prima della loro reale applicazione.
Le principali misure che si possono calcolare per esaminare i rendimenti sono: − la curva dei rendimenti cumulati: il grafico, la media, la varianza, …; − il grafico a barre di tutti i trades effettuati; − il massimo profitto; − la massima perdita; − la media dei trades profittevoli; − la media dei trades negativi; − l’incidenza di ciascun trades, in particolare quello che conduce al massimo profitto, sulla curva dei rendimenti; − il numero di trades vincenti consecutivi; − il numero di trades perdenti consecutivi;
− la frazione di trades profittevoli su quelli in perdita; Queste misure, rispetto alle prime, toccano maggiormente la psicologia dell’analista-trader, è bene perciò usarle con cautela ed eventualmente prendere alcuni accorgimenti per sottostimarle, in modo tale da frenare falsi entusiasmi. In alternativa, l’analista dovrebbe tener presente maggiormente le misure delle perdite, che non quelle dei profitti, più la varianza e la media della curva dei rendimenti, che non il profitto finale.
Successivo: 3.1 Dalle bandwidth al P-tree
Sommario: Index