Sono state eseguite numerose prove allo scopo di dimostrare l’abilità della kernel regression di trovare un modello per dati non lineari e multidimensionali.
In particolare, l’analisi descritta di seguito illustra le performance dell’applicazione nel fittare una variabile dipendente che ha il 10% di segnale ed il 90% di rumore (colonna 14°).
Si è scelto di mostrare i risultati di tale variabile nell’ipotesi che la serie finanziaria del Fib30 possa avere circa questa frazione di segnale. Si utilizzerà come criterio di modellamento (MC) la misura VR (Variance Reduction): la migliore performance che si potrà ottenere con qualsiasi tecnica di modellamento di una variabile dipendente con il 10% di segnale è VR=10%.
Non verranno mostrate tutte le analisi effettuate sulle varie serie con differenti frazioni di segnale, basti considerare che più la componente di segnale è forte, più il p-Tree riesce a classificare nettamente i vari pattern del learning set (nearest neighbors) nelle celle. In altre parole, più grande è la frazione di segnale più pattern si riusciranno ad individuare, dunque più celle si potranno costruire e la regressione potrà stimare al meglio i valori anche solo con pochi nearest neighbors, al contrario, se vi è molto rumore, la regressione dovrà considerare abbastanza nearest neighbors da riuscire a compensare il rumore di ogni punto di learning.
Si è proceduto inizialmente all’analisi della Fast Kernel Regression (FKR): kernel regression che utilizza il p-Tree per cercare i nearest neighbors (NUMNN) senza dover ricorrere al calcolo delle distanze e che successivamente stima y utilizzando solo i punti di learning di un’unica cella
(NUMCELL=1) pesandoli equamente con un unico kernel {NUMK=1, K(1)=1}.
La tabella mostra i risultati ottenuti con tale applicazione.
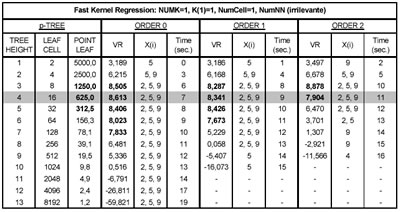
Osservando la tabella si può vedere che il massimo valore di VR si è ottenuto con l’algoritmo di ordine 2 (ORDER 2) e altezza del p-Tree pari a 3 (H=3), ciò nonostante l’algoritmo di ordine 0 (ORDER 0) conduce a valori di VR abbastanza elevati in minor tempo computazionale e meno dipendenti dall’altezza dell’albero (H={3,4,5}), inoltre sembra essere l’algoritmo che fallisce meno volte nell’individuazione dei tre best predictors (X2, X5, X9). Di seguito si mostra, a titolo d’esempio, il report di output della Fast Kernel Regression con H=4 e ORDER=0; i valori asteriscati corrispondono a parametri tenuti costanti in tutte le analisi eseguite.
DMIN - min number of dimensions : 1 (*) DMAX - max number of dimensions : 3 (*) NCP - number of candidate predictors : 10 (*) NCOL - number of columns of data : 18 (*) NREC - total number of records : 15000 (*) LTYPE - Learning set type (G, M, S) : S (*) G: growing, M: moving, S: static NUMCELL- Number of cells searched for NUMNN : 1 (*) NUMNN - Irrelevant because FAST mode specified STARTCP- starting variable : 1 (*) DELTA - Min incremental change : -100 (*) NODATA - For Ycalc : 999 (*) Kernel Regression parameters: MC - 1=VR, 2=CC, 3=CCO, : 1 (*) ORDER - 0 is average, 1 & 2 are surfaces : 0 FAST option used: Ycalc is cell average NUMK - Number of smoothing parameters : 1 (*) K(1) - Smoothing parameter 1 : 1.00 (*) YCOL - Column of dependent variable : 14 (*) Tree parameters: BUCKETSIZE - design number per cell (computed) : 625 TREEHEIGHT - tree parm : 4 Computed number of cells : 31 Computed number of leaf cells : 16 Computed avg bucket size : 625.0 Computed 2 Sigma limit for F Stat : 1.73 Data set parameters: NLRN - number of learning records : 10000 (*) NTST - number of test records : 5000 (*) NEVL - number of evaluation records : 0 (*) GAP - gap records between data sets : 0 (*) STARTLRN - starting learning record : 1 (*) STARTTST - starting test record : 10001 (*) Dim: 1 Var Red: -0.077 FracSS: 0.495 K: 1.00 X(1) = 1 Dim: 1 Var Red: 2.758 FracSS: 0.547 K: 1.00 X(1) = 2 Dim: 1 Var Red: -0.177 FracSS: 0.504 K: 1.00 X(1) = 3 Dim: 1 Var Red: -0.326 FracSS: 0.508 K: 1.00 X(1) = 4 Dim: 1 Var Red: 3.482 FracSS: 0.552 K: 1.00 X(1) = 5 Dim: 1 Var Red: -0.090 FracSS: 0.501 K: 1.00 X(1) = 6 Dim: 1 Var Red: -0.439 FracSS: 0.491 K: 1.00 X(1) = 7 Dim: 1 Var Red: -0.013 FracSS: 0.505 K: 1.00 X(1) = 8 Dim: 1 Var Red: 3.579 FracSS: 0.549 K: 1.00 X(1) = 9 Dim: 1 Var Red: -0.009 FracSS: 0.509 K: 1.00 X(1) = 10 Ordered results for 1 dimensional models: Total number of combinations: 10 (*) Number tested : 10 (*) survivenum(1) : 5 (*) Number of survivors : 5 Var Red: 3.579 FracSS: 0.549 X: 9 Var Red: 3.482 FracSS: 0.552 X: 5 Var Red: 2.758 FracSS: 0.547 X: 2
Var Red: -0.009 FracSS: 0.509 X: 10 Var Red: -0.013 FracSS: 0.505 X: 8 Dim: 2 Var Red: 2.971 FracSS: 0.549 K: 1.00 X(1) = 1 X(2) = 9 Dim: 2 Var Red: 5.267 FracSS: 0.543 K: 1.00 X(1) = 2 X(2) = 9 Dim: 2 Var Red: 3.064 FracSS: 0.550 K: 1.00 X(1) = 3 X(2) = 9 Dim: 2 Var Red: 3.184 FracSS: 0.550 K: 1.00 X(1) = 4 X(2) = 9 Dim: 2 Var Red: 6.172 FracSS: 0.553 K: 1.00 X(1) = 5 X(2) = 9 Dim: 2 Var Red: 3.013 FracSS: 0.549 K: 1.00 X(1) = 6 X(2) = 9 Dim: 2 Var Red: 2.672 FracSS: 0.549 K: 1.00 X(1) = 7 X(2) = 9 Dim: 2 Var Red: 3.004 FracSS: 0.549 K: 1.00 X(1) = 8 X(2) = 9 Dim: 2 Var Red: 3.046 FracSS: 0.549 K: 1.00 X(1) = 9 X(2) =10 Dim: 2 Var Red: 3.073 FracSS: 0.552 K: 1.00 X(1) = 1 X(2) = 5 Dim: 2 Var Red: 5.644 FracSS: 0.552 K: 1.00 X(1) = 2 X(2) = 5 Dim: 2 Var Red: 3.270 FracSS: 0.552 K: 1.00 X(1) = 3 X(2) = 5 Dim: 2 Var Red: 3.106 FracSS: 0.552 K: 1.00 X(1) = 4 X(2) = 5 Dim: 2 Var Red: 3.072 FracSS: 0.552 K: 1.00 X(1) = 5 X(2) = 6 Dim: 2 Var Red: 2.984 FracSS: 0.552 K: 1.00 X(1) = 5 X(2) = 7 Dim: 2 Var Red: 3.117 FracSS: 0.552 K: 1.00 X(1) = 5 X(2) = 8 Dim: 2 Var Red: 3.069 FracSS: 0.552 K: 1.00 X(1) = 5 X(2) =10 Dim: 2 Var Red: 2.258 FracSS: 0.547 K: 1.00 X(1) = 1 X(2) = 2 Dim: 2 Var Red: 2.291 FracSS: 0.547 K: 1.00 X(1) = 2 X(2) = 3 Dim: 2 Var Red: 2.228 FracSS: 0.546 K: 1.00 X(1) = 2 X(2) = 4 Dim: 2 Var Red: 2.331 FracSS: 0.547 K: 1.00 X(1) = 2 X(2) = 6 Dim: 2 Var Red: 2.039 FracSS: 0.548 K: 1.00 X(1) = 2 X(2) = 7 Dim: 2 Var Red: 2.176 FracSS: 0.547 K: 1.00 X(1) = 2 X(2) = 8 Dim: 2 Var Red: 2.304 FracSS: 0.547 K: 1.00 X(1) = 2 X(2) =10 Dim: 2 Var Red: -0.006 FracSS: 0.506 K: 1.00 X(1) = 1 X(2) =10 Dim: 2 Var Red: 0.025 FracSS: 0.511 K: 1.00 X(1) = 3 X(2) =10 Dim: 2 Var Red: -0.180 FracSS: 0.506 K: 1.00 X(1) = 4 X(2) =10 Dim: 2 Var Red: 0.054 FracSS: 0.507 K: 1.00 X(1) = 6 X(2) =10 Dim: 2 Var Red: -0.372 FracSS: 0.486 K: 1.00 X(1) = 7 X(2) =10 Dim: 2 Var Red: -0.057 FracSS: 0.504 K: 1.00 X(1) = 8 X(2) =10 Dim: 2 Var Red: -0.162 FracSS: 0.503 K: 1.00 X(1) = 1 X(2) = 8 Dim: 2 Var Red: -0.121 FracSS: 0.506 K: 1.00 X(1) = 3 X(2) = 8 Dim: 2 Var Red: -0.031 FracSS: 0.515 K: 1.00 X(1) = 4 X(2) = 8 Dim: 2 Var Red: -0.208 FracSS: 0.496 K: 1.00 X(1) = 6 X(2) = 8 Dim: 2 Var Red: -0.385 FracSS: 0.494 K: 1.00 X(1) = 7 X(2) = 8 Ordered results for 2 dimensional models: Total number of combinations: 45 (*) Number tested : 35 (*) survivenum( 2) : 5 (*) Number of survivors : 5 Var Red: 6.172 FracSS: 0.553 X: 5 9 Var Red: 5.644 FracSS: 0.552 X: 2 5 Var Red: 5.267 FracSS: 0.543 X: 2 9 Var Red: 3.270 FracSS: 0.552 X: 3 5 Var Red: 3.184 FracSS: 0.550 X: 4 9 Dim: 3 Var Red: 6.121 FracSS: 0.555 K: 1.00 X(1) = 1 X(2) = 5 X(3) = 9 Dim: 3 Var Red: 8.613 FracSS: 0.578 K: 1.00 X(1) = 2 X(2) = 5 X(3) = 9 Dim: 3 Var Red: 6.256 FracSS: 0.551 K: 1.00 X(1) = 3 X(2) = 5 X(3) = 9 Dim: 3 Var Red: 6.217 FracSS: 0.546 K: 1.00 X(1) = 4 X(2) = 5 X(3) = 9
Dim: 3 Var Red: 6.037 FracSS: 0.550 K: 1.00 X(1) = 5 X(2) = 6 X(3) = 9 Dim: 3 Var Red: 6.149 FracSS: 0.551 K: 1.00 X(1) = 5 X(2) = 7 X(3) = 9 Dim: 3 Var Red: 6.087 FracSS: 0.557 K: 1.00 X(1) = 5 X(2) = 8 X(3) = 9 Dim: 3 Var Red: 6.287 FracSS: 0.553 K: 1.00 X(1) = 5 X(2) = 9 X(3) = 10 Dim: 3 Var Red: 5.648 FracSS: 0.553 K: 1.00 X(1) = 1 X(2) = 2 X(3) = 5 Dim: 3 Var Red: 5.595 FracSS: 0.553 K: 1.00 X(1) = 2 X(2) = 3 X(3) = 5 Dim: 3 Var Red: 5.517 FracSS: 0.552 K: 1.00 X(1) = 2 X(2) = 4 X(3) = 5 Dim: 3 Var Red: 5.554 FracSS: 0.554 K: 1.00 X(1) = 2 X(2) = 5 X(3) = 6 Dim: 3 Var Red: 5.591 FracSS: 0.555 K: 1.00 X(1) = 2 X(2) = 5 X(3) = 7 Dim: 3 Var Red: 5.562 FracSS: 0.556 K: 1.00 X(1) = 2 X(2) = 5 X(3) = 8 Dim: 3 Var Red: 5.585 FracSS: 0.549 K: 1.00 X(1) = 2 X(2) = 5 X(3) = 10 Dim: 3 Var Red: 5.210 FracSS: 0.544 K: 1.00 X(1) = 1 X(2) = 2 X(3) = 9 Dim: 3 Var Red: 5.450 FracSS: 0.547 K: 1.00 X(1) = 2 X(2) = 3 X(3) = 9 Dim: 3 Var Red: 5.380 FracSS: 0.555 K: 1.00 X(1) = 2 X(2) = 4 X(3) = 9 Dim: 3 Var Red: 5.141 FracSS: 0.542 K: 1.00 X(1) = 2 X(2) = 6 X(3) = 9 Dim: 3 Var Red: 5.428 FracSS: 0.545 K: 1.00 X(1) = 2 X(2) = 7 X(3) = 9 Dim: 3 Var Red: 5.311 FracSS: 0.540 K: 1.00 X(1) = 2 X(2) = 8 X(3) = 9 Dim: 3 Var Red: 5.456 FracSS: 0.543 K: 1.00 X(1) = 2 X(2) = 9 X(3) = 10 Dim: 3 Var Red: 3.121 FracSS: 0.552 K: 1.00 X(1) = 1 X(2) = 3 X(3) = 5 Dim: 3 Var Red: 3.044 FracSS: 0.552 K: 1.00 X(1) = 3 X(2) = 4 X(3) = 5 Dim: 3 Var Red: 2.989 FracSS: 0.552 K: 1.00 X(1) = 3 X(2) = 5 X(3) = 6 Dim: 3 Var Red: 3.147 FracSS: 0.552 K: 1.00 X(1) = 3 X(2) = 5 X(3) = 7 Ordered results for 3 dimensional models: Total number of combinations: 120 (*) Number tested : 34 (*) survivenum(3) : 5 (*) Number of survivors : 5 Var Red: 8.613 FracSS: 0.578 X: 2 5 9 Var Red: 6.287 FracSS: 0.553 X: 5 9 10 Var Red: 6.256 FracSS: 0.551 X: 3 5 9 Var Red: 6.217 FracSS: 0.546 X: 4 5 9 Var Red: 6.149 FracSS: 0.551 X: 5 7 9 Best Model Report Fold 1 (Test Set Data): Model: 1 Var Red: 8.613 FracSS: 0.578 X: 2 5 9
Model: 2 Var Red: 6.287 FracSS: 0.553 X: 5 9 10 Timing Report: dim: 1 Num_spaces: 10 Time: 1 Time/space: 0.10 dim: 2 Num_spaces: 35 Time: 4 Time/space: 0.11 dim: 3 Num_spaces: 34 Time: 4 Time/space: 0.12 Total: Num_spaces: 79 Time: 9 Time/space: 0.11
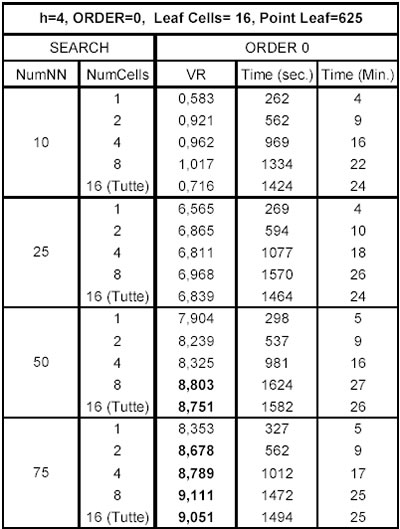
Si illustrano ora i risultati della kernel regression ad alta performance (KR) tenendo fissi i parametri H=4 e ORDER=0 e facendo variare il numero di celle adiacenti (NUMCELL) in cui effettuare la ricerca dei nearest neighbor il cui numero (NUMNN) viene fatto a sua volta variare.
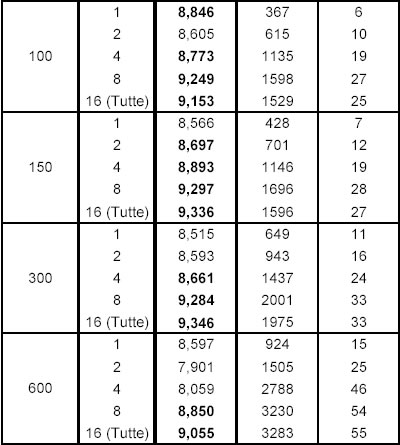
Osservando la tabella, riportata alla pagina successiva, si può notare che rispetto alla FKR con la KR si possono ottenere degli incrementi di VR considerevoli,ma anche fortissimi aumenti nella complessità computazionale evidenziati dal notevole tempo di elaborazione necessario (Time). Infatti, mentre il risultato migliore della FKR era pari a: VR=8,613 e Time=7 sec.; ora si vedono molti valori di VR superiori (valori in grassetto) la cui media è pari a 8,980, ma il tempo medio di calcolo richiesto per ottenerli è pari circa a 1.550 secondi, cioè circa 220 volte il tempo richiesto dalla FKR.
Rispetto alla FKR, con la KR si ottiene un aumento medio di VR del 4,26%, ma anche un incremento medio del tempo del 22042%. Con questo non si vuole dire che la KR sia una metodologia da scartare, dipende molto dall’operatività che si intende seguire nel trading mobiliare: l’utilizzo della KR può essere ottimo se si opera daily, ma rischioso se non pessimo quando l’operatività è intraday, in particolar modo quando l’affluenza dei dati è ad intervalli inferiori ai 30 minuti.
Successivo: 4.4 Un Approccio con le Reti Neurali Artificiali
Sommario: Index