Sul tempo associato al processo di modellamento si è già parlato nella sezione 3.1 in cui si affermava che il tempo necessario per sviluppare un set di modelli è proporzionale al prodotto tra il numero di spazi esaminati e il tempo medio richiesto ad ogni spazio:

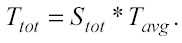
Questa formula è basata sull’ipotesi che il computer usato abbia un singolo processore. In ogni caso, si possono estendere le nozioni già enunciate e quelle che verranno presentate successivamente all’eventualità che il computer utilizzato possieda più processori. Oggi infatti, si possono trovare in commercio calcolatori con 2, 4 e perfino 8 processori in parallelo. In tal caso, teoricamente, il tempo totale necessario all’elaborazione (Ttot) si ridurrebbe di un fattore pari a N, dove N è il numero di processori disponibili.

Il tempo computazionale, inoltre, può essere condizionato da molteplici varianti come per esempio la quantità ed il tipo di memoria RAM, la presenza o meno di cooprocessori matematici, il tipo di sistema operativo e l’integrità del sistema.

La trattazione di tutti questi fattori esula, però, lo scopo generale del paragrafo, che è semplicemente quello di stimare approssimativamente il tempo di calcolo della kernel regression, senza aver la pretesa di basare le strategie di modellamento su equazioni teoriche inerenti la complessità computazionale: gran parte del lavoro è empirico e la teoria funge solo da supporto.

Nell’applicare modelli di kernel regression ad alta performance con l’utilizzo del p-Tree, il tempo medio per spazio (Tavg) può essere considerato come la somma di due componenti base: il tempo di preparazione (preparation time) ed il tempo di elaborazione (run time):

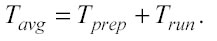
Il tempo di preparazione: T_prep Il tempo di preparazione è formato da tre componenti: il tempo indispensabile per gli ordinamenti o sort time (T_sort), il tempo necessario per sviluppare la matrice di adiacenza (T_adj) se vengono usate le celle adiacenti per trovare i nearest neighbors, ed infine il tempo richiesto per salvare il registro (bookkeeping) di tutti i nodi del p-Tree (T_book):

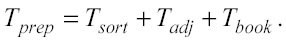
− Di (T_sort) si è già parlato nella sezione 3.2 ed è proporzionale ad H ed a nlrn:

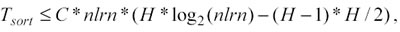
−T_adjè il tempo dovuto per la costruzione della matrice di adiacenza ed è pari a zero nell’unico caso in cui viene usata solo la cella dove risiede il punto di test per trovare i punti più vicini. Tuttavia, se la matrice di adiacenza è richiesta (numcells >1), T_adj è un termine importante e per elevati valori di H può diventare la quantità dominante di T_prep. T_adj infatti, è proporzionale al quadrato del numero delle “celle foglie” (2_2h), in altre parole, al crescere del valore H di un’unità, T_adj aumenta di un fattore pari a quattro:

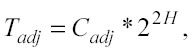
Se il numero di learning points per ogni cella (ppc) è tenuto costante, allora si può relazionare H con nlrn:

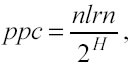
moltiplicando entrambe le proposizioni per 2^H e poi facendo il logaritmo in base due, si scopre che H cresce proporzionalmente a log₂(nlrn), si otterrà:

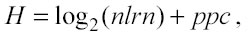
con ppc costante e dunque

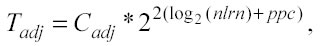
confrontando questa espressione con quella del Sort Time:

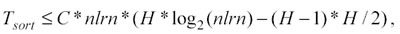
se ne deduce che per grandi valori di nlrn, T_sort diventa piccolo rispetto a T_adj, sempre che venga calcolata la matrice di adiacenza ( T_adj >0 ).

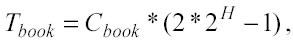
ma se i punti per cella sono costanti si ha:

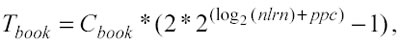
dunque T_book aumenta meno velocemente rispetto a T_sort e T_adj.

Sintetizzando, raddoppiando nlrn, per mantenere costante ppc si dovrà aumentare H di un’unità, così facendo T_book crescerà di un fattore circa uguale a 2, T_sort aumenterà di un fattore leggermente più grande di 2 e T_adj si prolungherà di un fattore pari a 4. Allora per elevati valori di nlrn il termine dominante nella complessità computazionale di pre-analisi (T_prep) è T_adj se T_adj ≠ 0.

Il tempo di elaborazione: T_run

Il tempo di elaborazione T_run è proporzionale al numero di test points:

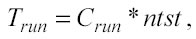
dove C_run è una costante che indica il tempo di elaborazione per un singolo punto di test e dipende dai parametri che si utilizzano nel modellamento. I principali elementi che concorrono a determinare C_run sono quattro:

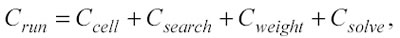
C_celè il tempo impiegato per localizzare la cella in cui risiede il test point, è proporzionale ad H ed ha una durata molto breve.

− C_search rappresenta il tempo necessario per cercare i numnn nearest neighbors, può essere pari a zero oppure può rappresentare la componente dominante di C_run . È uguale a zero se vengono usati solo i learning points della cella in cui risiede il punto di test per stimare j . Se, invece, viene eseguita una ricerca, C_search è proporzionale al prodotto tra il numero di celle incluse nella ricerca (numcells) e i punti di ogni cella (ppc), inoltre dipende dal numero di nearest neighbors da trovare (numnn).

−C_weight è legato al tempo indispensabile per determinare i pesi da assegnare ad ogni nearest neighbors, è proporzionale a numnn a meno che tutti i punti non siano equamente pesati, in tal caso C_weight risulta pari a zero.

− C_solve rappresenta il tempo richiesto per calcolare i valori di j con l’algoritmo della kernel regression e dipende dall’ordine e dalla dimensionalità del polinomio utilizzato. Se l’ordine è 0 vi è un’unica equazione ad un’incognita, se l’ordine è 1 le equazioni da trovare sono p+1, mentre se l’ordine è 2 il numero di equazioni è

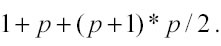
. Il tempo necessario per risolvere le equazioni è approssimativamente proporzionale al numero di equazioni elevato alla terza potenza (num_equations3), mentre il tempo necessario all’ultimo stadio (la stima di j yˆ) è minore rispetto a quello richiesto per risolvere le equazioni ed è proporzionale a num_equations. Da quanto detto sulle componenti di C_run, le condizioni da rispettare per ridurre al minimo il tempo di elaborazione sono:

− ricorrere solo ai learning points localizzati nella cella in cui è caduto il punto di test con la conseguenza che C_search=0;

− pesare tutti i punti equamente in modo che C_weight=0;

− quando dei punti di learning vengono aggiunti o tolti da una cella (learning set dinamico: growing e moving option), ricalcolare i coefficienti solo dopo che un nuovo punto di test viene posto nella cella. Quando si usano queste strategie, il tempo di elaborazione T_run si riduce notevolmente e di solito diventa più breve del tempo di preparazione T_prep, che a sua volta si abbrevia per il fatto che non è necessario definire la matrice di adiacenza (T_adj = 0). Questo veloce criterio di modellamento è chiamato Fast Kernel Regression ed è utilizzato soprattutto quando tra efficacia ed efficienza del modello si predilige l’efficienza, quando cioè, a piccoli scostamenti nel miglioramento della performance del modello, si preferiscono più elevati scostamenti in termini di riduzione di tempo nel raggiungere i risultati. La Fast Kernel Regression sembra dunque un metodo ideale nel caso di operatività intraday nei mercati finanziari: un modello che apprende ed elabora velocemente i dati di input può essere in grado di fare previsioni con un ritardo sostenibile rispetto alla frequenza d’aggiornamento dei dati (15’, 10’, 5’, 1’, Tick).

Monico Dino

Successivo: 3.5 Il tempo pesa i dati

Sommario: Index