La kernel regression è operativamente simile alle reti neurali, tuttavia, in dettaglio le due metodologie sono totalmente differenti, ma abbastanza complementari.
Un approccio che combina le migliori caratteristiche della kernel regression con quelle delle reti neurali può aiutare l’analista a sviluppare un buon modello.
Le due tecnologie vengono applicate entrambe nei problemi in cui non si conosce né il modello matematico sottostante né tanto meno se è possibile sviluppare un modello robusto utilizzando i candidate predictors. Lo scopo del processo di modellamento è quello di riuscire a predire una variabile di output basata su un set di candidate predictors.
Il tipico approccio con KR e NN è basato su due paradigmi: training e testing. Ogni modello è basato sul training set e successivamente è testato con l’utilizzo del testing set. Mentre le reti neurali modellano con processi iterativi, nei quali i pesi associati tra gli input e gli output di un neurone sono modificati fino a che non viene raggiunto un certo livello di performance, il metodo della kernel regression non è iterativo.
Dal punto di vista computazionale quanto detto implica che il processo di training con le reti neurali è molto lungo, ma una volta che il sistema converge ad un modello, il processo di testing è molto rapido. Viceversa con KR il processo di learning è estremamente rapido ed il tempo di testing può essere altrettanto rapido se si sacrifica un po’ di performance (FKR), tuttavia utilizzando tutte le potenzialità di KR può diventare molto lento (vedi cap. 3.4).
La natura complementare delle due tecnologie può essere riassunta nella tabella seguente, in cui si mostra le relazioni tra la qualità del modello, il tempo di training e quello di testing rispettivamente nelle reti neurali (NN) e nella kernel regression (KR).
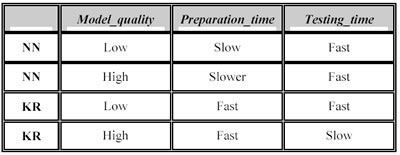
La qualità del modello è specificata dall’analista attraverso l’utilizzo dei parametri e i loro differenti valori. Con le reti neurali l’analista può alterare la qualità del modello cambiando l’architettura della rete (il numero di neuroni, il numero di strati nascosti, le funzioni di attivazione, la funzione d’apprendimento…). Allo stesso modo ci sono dei parametri della kernel regression che possono alterare la qualità del modello: l’ordine dell’algoritmo, la dimensione massima del polinomio, l’altezza massima del p-Tree o il numero di punti per cella, il modo di ricerca dei nearest neighbors (si veda il cap. 4.2).
Per quanto riguarda la bontà dei modelli individuati dalle due metodologie, si può dire che con la matrice dati proposta (cap. 4.1) la KR ha portato a risultati migliori rispetto alla NN, ma la relazione tra performance e valori assunti dai parametri della kernel regression è stata più visibile, ciò comporta per l’analista un maggior controllo sui parametri.
In generale, senza bocciare l’approccio alle reti neurali, per problemi ad alta dimensionalità con serie storiche molto lunghe, la strategia di modellamento diventa:
1. applicare una veloce tecnica di ricerca come la FKR per identificare gli spazi più promettenti;
2. utilizzare la KR oppure le NN per esaminare gli spazi più promettenti in dettaglio.
Questo tipo di approccio dovrebbe dare al data miner una probabilità maggiore di successo nel modellare serie storiche come quelle dei mercati finanziari, in particolare il Fib30 o il MiniFib30.
Successivo: Appendice Email
Sommario: Index