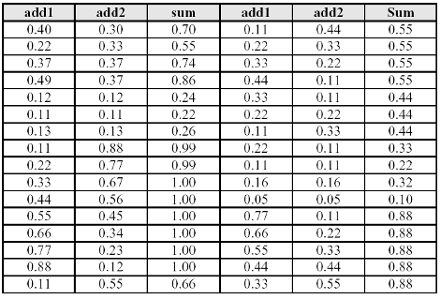
Utilizziamo il training set di fig.8 che contiene 40 esempi normalizzati di somma di due numeri: il programma presentato in questo capitolo, su una SPARK station, è arrivato al raggiungimento del target 0.05 dopo pochi minuti, in circa 4300 epoche con un epsilon(tasso di apprendimento)=0.5 e con quattro neuroni per ogni strato intermedio(ovviamente n_input=2 e n_output=1).

Il raggiungimento del target_error 0.02 è stato ottenuto nelle stesse condizioni all'epoca ~13800. Se non volete attendere molto tempo e verificare ugualmente la convergenza della rete potete ridurre il training set a 10 o 20 esempi curando che siano adeguatamente distribuiti (8 è dato dalla somma 1+7 ma anche 4+4 e 7+1).

Con un training set ridotto la rete converge molto più velocemente ma è chiaro che il potere di generalizzazione risulta inferiore, per cui presentando poi alla rete degli esempi fuori dal training set l'errore ottenuto potrebbe essere molto più elevato del target_error raggiunto. `É buona norma lavorare con delle pause su un numero di epoche non elevato al fine di poter eventualmente abbassare il tasso di apprendimento epsilon quando ci si accorge della presenza di oscillazioni(errore che aumenta e diminuisce alternativamente) dovute a movimenti troppo lunghi(epsilon alto) intorno ad un minimo (che speriamo sia il target e non un minimo locale).

Il raggiungimento del target 0.02 è relativamente rapido mentre da questo punto in poi la discesa verso il minimo è meno ripida e i tempi diventano più lunghi(è il problema della discesa del gradiente con movimenti inversamente proporzionali alla derivata nel punto). Inoltre avvicinandosi al minimo è prudente utilizzare un epsilon basso per il motivo esaminato prima.

È sicuramente possibile che un errore target non sia raggiungibile in tempi accettabili se è troppo basso in relazione alla complessità del problema. In ogni caso bisogna ricordare che le reti neurali non sono sistemi di calcolo precisi ma sistemi che forniscono risposte approssimate a inputs approssimati. Se ripetete due o più volte lo stesso training con gli stessi dati e gli stessi parametri potreste sicuramente notare differenze di tempi di convergenza verso il target dovuti al fatto che inizialmente i pesi della rete sono settati a valori random (procedura weight_starter) che possono essere più o meno favorevoli alla soluzione del problema.

Nella fig.9 è visualizzato il know_how di una rete con un neurone nello strato hidden1 e due neuroni nello strato hidden2, dopo l'addestramento alla somma fino al target_error=0.05: sono evidenziati i numeri che rappresentano i pesi dei collegamenti.

 

Luca Marchese

Successivo: Un esempio applicativo

Sommario: Indice