Uno degli scopi fondamentali dell’analisi classica delle serie temporali è quello di scomporre la serie nelle sue componenti, isolandole per poterle studiare meglio. Inoltre, per poter applicare l’approccio stocastico (modelli AR, MA, ARIMA) alle serie storiche è quasi sempre necessario eliminare il trend e la stagionalità al fine di avere un processo stazionario. Le componenti di una serie storica di solito sono le seguenti: trend, stagionalità, ciclo, residua o erratica. Esse possono essere legate tra loro in modo additivo:
Yt=Tt + Ct + St + Et
oppure in modo moltiplicativo:
Yt=Tt * Ct * St * Et
Un modello di tipo moltiplicativo può essere facilmente trasformato in un modello additivo usando l’operatore logaritmo:
log(Yt)=log(Tt )+ log(Ct)+ log(St)+ log(Et)
La componente stagionale è presente nel caso di serie storiche infrannuali (mensili, trimestrali, etc.), mentre il ciclo è tipico delle serie storiche che descrivono dei fenomeni economici in un periodo di osservazione piuttosto lungo. Spesso, quando non è particolarmente evidente, la componente ciclica viene considerata all’interno della componente di fondo. Per la stima del trend si ricorre di solito a funzioni tipiche come la retta (trend lineare), la parabola (trend parabolico), un polinomio di grado k, l’esponenziale (trend esponenziale), la logistica e via discorrendo. Tali funzioni sono quasi tutte lineari o comunque linearizzabili attraverso opportune trasformazioni.
Stima delle componenti
Medie mobili, differenze dei termini
Oltre al metodo analitico per la stima del trend, ci sono metodi più elementari anche se meno raffinati per detrendizzare una serie temporale: la perequazione meccanica con medie mobili e l’applicazione dell’operatore differenza. Nel caso delle medie mobili si pone il problema dell’esatta determinazione del numero dei termini da usare. In genere il trend può essere stimato con un’opportuna ponderazione dei valori della serie:

Il package ast mette a disposizione la funzione sfilter():

Si è applicata ai dati originari una media mobile ponderata a 13 termini per eliminare la stagionalità e mettere in risalto solo la componente di fondo. Per ottenere una visualizzazione grafica Graf.1/b):
plot(ore.filt, main="Trend stimato con la media mobile")
In alternativa si può usare la funzione filter() presente nel package stats, fissando il parametro filter al valore corrispondente ad una serie mensile (1/25 per 25 volte per un valore di a=12 come dalla formula di sopra dei filtri lineari).


e ne tracciamo il grafico (Graf. 1/b):
plot(ore.fil2, main="Trend stimato con media mobile - funzione 'filter'")
Trend stimato con media mobile - funzione 'sfilter'

Trend stimato con media mobile - funzione 'filter'

Un ulteriore metodo per eliminare il trend è quello di operare sulle differenze tra i termini (o i logaritmi dei termini in caso di modello moltiplicativo) della serie storica: le differenze del primo ordine rimuovono un trend lineare, quelle del secondo ordine un trend parabolico, quelle di ordine k rimuovono un trend polinomiale di grado k:

Il comando di R per applicare tale metodo è: diff.ts()che consente di operare le differenze del primo ordine e in generale, usato ripetitivamente, le differenze di qualsiasi ordine.
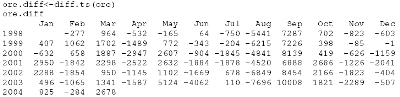
plot(ore.diff,main="Serie delle ore lavorate detrendizzata")

Vito Ricci
Successivo: Livellamento esponenziale con il metodo di Holt-Winters
Sommario: Index