
La libreria ast mette a disposizione un’ulteriore funzione per la decomposizione di una serie temporale: si tratta del comando tsr()che permette di stimare una serie di modelli del tipo:
(serie osservata) = f(trend, stagionalità, residuo)
che può essere adoperata sia modelli addittivi che per quelli moltiplicativi, inoltre prevede l’utilizzo di diversi stimatori per calcolare la componente di trend. Gli stimatori, detti smoothers (sovente tradotto in italiano con “lisciatori”), riconosciuti sono:
-constant: la serie “lisciata” assume valore uguale alla media della serie osservata per ogni istante di tempo;
- poly(r): la serie osservata viene interpolata con un polinomio di grado r;
- loess(r,g): la serie osservata è “lisciata” utilizzando una regressione locale di tipo loess; r è il grado del polinomio utilizzato; g è (approssimativamente) il numero di parametri equivalenti desiderati;
- gauss(r,g): la serie osservata è “lisciata” utilizzando una regressione locale con pesi gaussiani (ovvero la funzione peso è la densità di una normale di media nulla); r è il grado del polinomio utilizzato; g è (approssimativamente) il numero di parametri equivalenti desiderati
- spline(g): la serie osservata è “lisciata” utilizzando una spline con (approssimativamente) g parametri equivalenti. Tale funzione risulta essere alquanto flessibile per le diverse possibilità offerta. La scelta dello stimatore migliore può essere fatta con l’ausilio dei grafici.
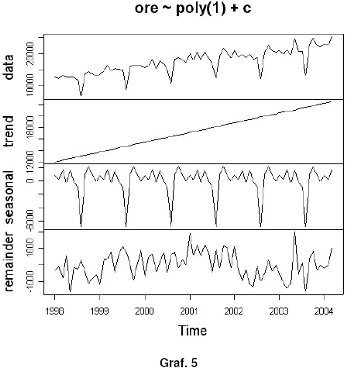
Utilizziamo la funzione tsr() per stimare le componenti della nostra serie di ore lavorate ipotizzando un trend lineare con stagionalità costante:
library(ast)
tsr.fit<-tsr(ore~poly(1)+c)

per aver una visualizzazione grafica del modello stimato (Graf. 5)
plot(tsr.fit)
Proviamo a vedere il grado di adattamento di questo tipo trend tracciando il grafico della serie filtrata (ore.filt) sovrapposto al trend stimato con tsr()(Graf. 6)
plot(ore.filt)
lines(trend(tsr.fit),col="red")

Come si può facilmente vedere l’adattamento non è particolarmente buono. Ciò ci induce ad utilizzare un altro tipo di “lisciatore”, ad esempio di tipo loess(r,g).
tsr2.fit<-tsr(ore~loess(1,10))
plot(ore.filt)
lines(trend(tsr2.fit),col="red")
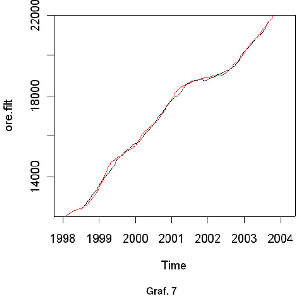
Il risultato è decisamente migliore (Graf. 7). Per determinare il numero dei parametri equivalenti spesso si deve procedere per tentativi: in genere aumentando il numero dei parametri equivalenti il grado di adattamento migliora. Confrontiamo i trend stimati con i tre metodi (decompose()in rosso, stl()in blu, tsr() in nero):
plot(trend(tsr2.fit),main="Comparazione del trend stimato")
lines(ore.filt, col="red")
lines(trend.stl, col="blue")
Come si vede I tre trend sono all’incirca tutti equali e nel grafico si sovrappongono abbondantemente (Graf. 7)
Vito Ricci
Successivo: Metodo analitico III
Sommario: Index