Il metodo di riduzione della varianza noto come tecnica della variabile di controllo si fonda sullo stesso principio della tecnica delle variabili antitetiche, di cui costituisce una generalizzazione in quanto utilizza una quantità che varia “assieme” alla variabile di interesse. E’ uno dei metodi più utilizzati e si basa sull’idea “use what you know” che, per valutare qualcosa di “sconosciuto” (obiettivo), si può procedere nella valutazione di un altro obiettivo simile (la variabile di controllo) ma completamente conosciuto.
Per esempio se il prodotto finanziario che si vuole valutare è complesso si può procedere alla valutazione un prodotto simile di cui esiste la soluzione in forma chiusa lasciando che il metodo Monte Carlo determini la differenza di valore. Il metodo sostituisce il valore atteso (da stimare) della variabile casuale Z (ad esempio il payoff di un’opzione a sua volta funzione della variabile casuale X) con la seguente quantità da stimare:
 in cui W è anch’essa una trasformata di X ma il cui valore atteso teorico è noto.
Stimando in simulazione la precedente quantità si ottiene:
in cui W è anch’essa una trasformata di X ma il cui valore atteso teorico è noto.
Stimando in simulazione la precedente quantità si ottiene:
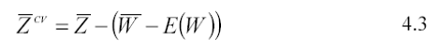
Dove 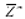 è uno stimatore della media E(Z) a partire dallo stimatore diretto di E(Z)
corretto per una stima dell’errore (W-E(W)) utilizzata come quantità di controllo.
Un esempio classico di applicazione di tale tecnica si ha nel caso di valutazione
di opzioni asiatiche, le quali richiedono la media dei prezzi del sottostante per il calcolo
del payoff.
è uno stimatore della media E(Z) a partire dallo stimatore diretto di E(Z)
corretto per una stima dell’errore (W-E(W)) utilizzata come quantità di controllo.
Un esempio classico di applicazione di tale tecnica si ha nel caso di valutazione
di opzioni asiatiche, le quali richiedono la media dei prezzi del sottostante per il calcolo
del payoff.
Essendo disponibile una soluzione in forma chiusa solo nel caso in cui la media sia di tipo geometrico, si utilizza tale opzione come variabile di controllo per valutare un’opzione il cui payoff consideri invece una media di tipo aritmetico.
Di R. Casarin & M. Gobbo
Successivo: Tecnica del campionamento stratificato
Sommario: Indice