Il metodo di riduzione della varianza noto come tecnica di campionamento Latin Hypercube si presenta come estensione al caso d-dimensionale del metodo del campionamento stratificato. Tale metodo consente una riduzione della varianza dello stimatore poiché, in modo del tutto simile al metodo del campionamento stratificato permette di rappresentare in modo più efficiente l’insieme di definizione d-dimensionale della variabile casuale da cui si sta simulando.

In simulazione, per ogni intervallo ddimensionale viene estratto casualmente un insieme di osservazioni campionarie in modo che ad ogni intervallo d-dimensionale corrisponda ad un’area della distribuzione di probabilità di uguale valore (intervalli equiprobabili). Un primo modo di estendere la tecnica del campionamento stratificato al caso di simulazione d-dimensionale consiste nel ripartire l’insieme di supporto della variabile casuale su ogni dimensione in n intervalli. In questo modo vengono generati nd ipercubi. Generata una successione di vettori d-dimensionali di variabili casuali uniformi:

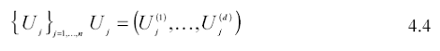
si applica una trasformazione di variabile che consente di ottenere un vettore di variabili casuali uniformemente distribuite in ciascuno degli nd intervalli d-dimensionali: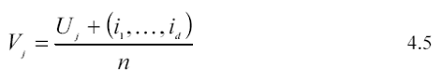

in cui ik =0,1, 2,...,n-1 rappresenta l’estremo inferiore dell’i-esimo intervallo nella dimensione k-esima, con k =1,2,...,d .

Il primo problema che si presenta in questo metodo è dato dalla complessità computazionale dovuta all’elevato numero di intervalli (nd ) che occorre generare, tranne il caso in cui n sia molto “piccolo”. Il secondo problema è la dipendenza tra gli elementi casuali del vettore. La stratificazione induce infatti un ordinamento crescente nella successione delle osservazioni simulate dalla distribuzione uniforme.

Questo ordinamento si ripete in ciascuna dimensione del vettore casuale generando quindi una dipendenza tra gli elementi dello stesso. Per evitare questi problemi viene introdotto il metodo detto Latin Hypercube. Esso può essere definito come un metodo di generazione casuale d-dimensionale che consente di mantenere le condizioni di regolarità introdotte dalla stratificazione in sottointervalli. Il metodo di simulazione Latin Hypercube comporta:

A) la ripartizione dell’insieme di supporto d-dimensionale in una successione di intervalli (nd) disgiunti, in cui n rappresenta il numero di sotto-intervalli per ciascuna delle d dimensioni. Si suppone, per semplicità che ciascuna dimensione sia scomposta in un numero uguale di sotto-intervalli;

B) la costruzione di una successione di n variabili casuali distribuite secondo f(X) in ogni intervallo. Sia quindi data una successione di n vettori di variabili casuali uniformi (0,1)d:

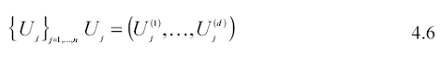
mediante la seguente trasformazione è possibile ottenere una successione di n vettori di variabili casuali uniformi definite su ciascun intervallo d-dimensionale:

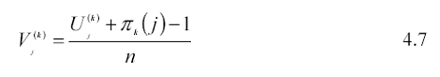
con j= 1,2,...,n, K = 1,2,...,d e dove la successione (π1,...,πd) è costituita da permutazioni casuali indipendenti relative all’insieme {1,...n } ed ognuna uniformemente distribuita sull’intervallo (0,n!) . La randomizzazione assicura che ciascun vettore Vj sia uniformemente distribuito sull’ipercubo d-dimensionale. La seguente ulteriore trasformazione consente di ottenere una successione di n vettori di variabili casuali d-dimensionali distribuite secondo f(X) su ogni intervallo:

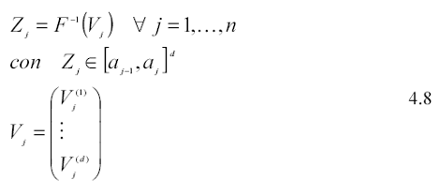
C) La scelta del numero m di osservazioni da simulare per ciascun intervallo. Sia N il numero di simulazioni che si vogliono ottenere. La relazione tra il numero di sotto-intervalli per ciascuna dimensione (n), il numero di simulazioni per sottointervallo (m) ed il numero complessivo di simulazioni (N) è dato da:

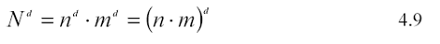
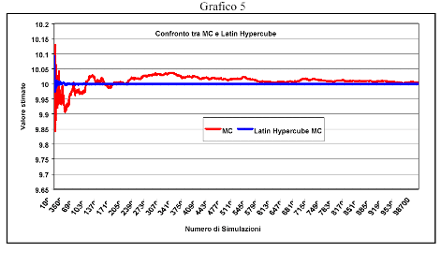
Si presenta un confronto tra i metodi Monte Carlo e Latin Hypercube applicati alla stima della media della funzione

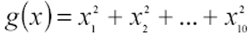
Osserviamo che le variabili casuali

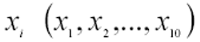
si distribuiscono come normali standardizzate, con matrice di correlazione diagonale in quanto le 10 variabili casuali sono indipendentemente distribuite.

Inoltre avremo che

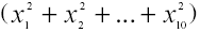
si distribuisce come una chi-quadro con 10 gradi di libertà. Quindi la variabile casuale g(x) ha media teorica 10 e varianza teorica 2*10=20.

La stima della media di g(x) si ottiene simulando i valori della variabile casuale x di dimensione 10, calcolando il valore di g(x) e facendo la media su tutte le simulazioni. Le simulazioni (in numero crescente da 100 a 100.000) sono effettuate con i metodi Monte Carlo e campionamento Latin Hypercube.

Di R. Casarin & M. Gobbo

 

Successivo: Tecnica del campionamento degenere

Sommario: Indice