The class of generalized linear models handled by facilities supplied in R includes gaussian, binomial, poisson, inverse gaussian and gamma response distributions and also quasi-likelihood models where the response distribution is not explicitly specified. In the latter case the variance function must be specified as a function of the mean, but in other cases this function is implied by the response distribution. Each response distribution admits a variety of link functions to connect the mean with the linear predictor. Those automatically available are shown in the following table:

The combination of a response distribution, a link function and various other pieces of information that are needed to carry out the modeling exercise is called the family of the generalized linear model.
The glm() function
function only, the same mechanism as was used for linear models can still be used to specify the linear part of a generalized model. The family has to be specified in a different way. The R function to fit a generalized linear model is glm() which uses the form
> fitted.model <- glm(formula, family=family.generator, data=data.frame)
The only new feature is the family.generator, which is the instrument by which the family is described. It is the name of a function that generates a list of functions and expressions that together define and control the model and estimation process. Although this may seem a little complicated at first sight, its use is quite simple. Where there is a choice of links, the name of the link may also be supplied with the family name, in parentheses as a parameter. In the case of the quasi family, the variance function may also be specified in this way. Some examples make the process clear.
The gaussian family
A call such as
> fm <- glm(y ~ x1 + x2, family = gaussian, data = sales)
achieves the same result as
> fm <- lm(y ~ x1+x2, data=sales)
but much less efficiently. Note how the gaussian family is not automatically provided with a choice of links, so no parameter is allowed. If a problem requires a gaussian family with a nonstandard link, this can usually be achieved through the quasi family, as we shall see later.
The binomial family
Consider a small, artificial example, from Silvey (1970). On the Aegean island of Kalythos the male inhabitants suffer from a congenital eye disease, the effects of which become more marked with increasing age. Samples of islander males of various ages were tested for blindness and the results recorded. The data is shown below:
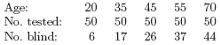
The problem we consider is to fit both logistic and probit models to this data, and to estimate for each model the LD50, that is the age at which the chance of blindness for a male inhabitant is 50%.
If y is the number of blind at age x and n the number tested, both models have the form
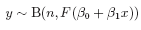
where for the probit case, F(z) = Φ(z) is the standard normal distribution function, and in the logit case (the default), F(z) = ez/(1 + ez). In both cases the LD50 is
LD50 = −β0/ β1
that is, the point at which the argument of the distribution function is zero. The first step is to set the data up as a data frame
> kalythos <- data.frame(x = c(20,35,45,55,70), n = rep(50,5), y = c(6,17,26,37,44))
To fit a binomial model using glm() there are three possibilities for the response:
• If the response is a vector it is assumed to hold binary data, and so must be a 0/1 vector.
• If the response is a two-column matrix it is assumed that the first column holds the number of successes for the trial and the second holds the number of failures.
• If the response is a factor, its first level is taken as failure (0) and all other levels as ‘success’ (1).
Here we need the second of these conventions, so we add a matrix to our data frame:
> kalythos$Ymat <- cbind(kalythos$y, kalythos$n - kalythos$y)
To fit the models we use
> fmp <- glm(Ymat ~ x, family = binomial(link=probit), data = kalythos)
> fml <- glm(Ymat ~ x, family = binomial, data = kalythos)
Since the logit link is the default the parameter may be omitted on the second call. To see the results of each fit we could use
> summary(fmp)
> summary(fml)
Both models fit (all too) well. To find the LD50 estimate we can use a simple function:
> ld50 <- function(b) -b[1]/b[2]
> ldp <- ld50(coef(fmp)); ldl <- ld50(coef(fml)); c(ldp, ldl)
The actual estimates from this data are 43.663 years and 43.601 years respectively.
Poisson models
With the Poisson family the default link is the log, and in practice the major use of this family is to fit surrogate Poisson log-linear models to frequency data, whose actual distribution is often multinomial. This is a large and important subject we will not discuss further here. It even forms a major part of the use of non-gaussian generalized models overall. Occasionally genuinely Poisson data arises in practice and in the past it was often analyzed as gaussian data after either a log or a square-root transformation. As a graceful alternative to the latter, a Poisson generalized linear model may be fitted as in the following example:
> fmod <- glm(y ~ A + B + x, family = poisson(link=sqrt), data = worm.counts)
Quasi-likelihood models
For all families the variance of the response will depend on the mean and will have the scale parameter as a multiplier. The form of dependence of the variance on the mean is a characteristic of the response distribution; for example for the poisson distribution Var[y] = µ.
For quasi-likelihood estimation and inference the precise response distribution is not specified, but rather only a link function and the form of the variance function as it depends on the mean. Since quasi-likelihood estimation uses formally identical techniques to those for the gaussian distribution, this family provides a way of fitting gaussian models with non-standard link functions or variance functions, incidentally. For example, consider fitting the non-linear regression
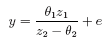
which may be written alternatively as
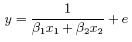
where x1 = z2/z1, x2 = −1/x1, β1 = 1/θ1 and β2 = θ2/θ1. Supposing a suitable data frame to be set up we could fit this non-linear regression as
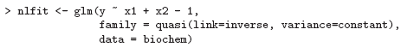
The reader is referred to the manual and the help document for further information, as needed.
Next: Nonlinear least squares and maximum likelihood models
Summary: Index