Statistical models in R

This section presumes the reader has some familiarity with statistical methodology, in particular with regression analysis and the analysis of variance. Later we make some rather more ambitious presumptions, namely that something is known about generalized linear models and nonlinear regression. The requirements for fitting statistical models are sufficiently well defined to make it possible to construct general tools that apply in a broad spectrum of problems. R provides an interlocking suite of facilities that make fitting statistical models very simple. As we mention in the introduction, the basic output is minimal, and one needs to ask for the details by calling extractor functions.

Defining statistical models; formulae

The template for a statistical model is a linear regression model with independent, homoscedastic errors

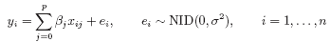
In matrix terms this would be written

y = Xβ + e

where the y is the response vector, X is the model matrix or design matrix and has columns x0, x1, . . . , xp, the determining variables. Very often x0 will be a column of ones defining an intercept term.

Examples

y ~ x

y ~ 1 + x

Both imply the same simple linear regression model of y on x. The first has an implicit intercept term, and the second an explicit one.

y ~ 0 + x

y ~ -1 + x

y ~ x - 1

Simple linear regression of y on x through the origin (that is, without an intercept term).

log(y) ~ x1 + x2 Multiple regression of the transformed variable, log(y), on x1 and x2 (with an implicit intercept term).

y ~ poly(x,2) y ~ 1 + x + I(x^2)

Polynomial regression of y on x of degree 2. The first form uses orthogonal polynomials, and the second uses explicit powers, as basis.

y ~ X + poly(x,2)

Multiple regression y with model matrix consisting of the matrix X as well as polynomial terms in x to degree 2.

y ~ A

Single classification analysis of variance model of y, with classes determined by A.

y ~ A + x Single classification analysis of covariance model of y, with classes determined by A, and with covariate x.

y ~ A*B

y ~ A + B + A:B

y ~ B %in% A

y ~ A/B

Two factor non-additive model of y on A and B. The first two specify the same crossed classification and the second two specify the same nested classification. In abstract terms all four specify the same model subspace.

y ~ (A + B + C)^2

y ~ A*B*C - A:B:C

Three factor experiment but with a model containing main effects and two factor interactions only. Both formulae specify the same model.

y ~ A * x

y ~ A/x

y ~ A/(1 + x) - 1

Separate simple linear regression models of y on x within the levels of A, with different codings. The last form produces explicit estimates of as many different intercepts and slopes as there are levels in A.

y ~ A*B + Error(C)

An experiment with two treatment factors, A and B, and error strata determined by factor C. For example a split plot experiment, with whole plots (and hence also subplots), determined by factor C.

The operator ~ is used to define a model formula in R. The form, for an ordinary linear model, is

response ~ op_1 term_1 op_2 term_2 op_3 term_3 ...

where

response

is a vector or matrix, (or expression evaluating to a vector or matrix) defining the response variable(s).

op i

is an operator, either + or -, implying the inclusion or exclusion of a term in the model, (the first is optional).

term i

is either

• a vector or matrix expression, or 1,

• a factor, or

• a formula expression consisting of factors, vectors or matrices connected by formula operators.

In all cases each term defines a collection of columns either to be added to or removed from the model matrix. A 1 stands for an intercept column and is by default included in the model matrix unless explicitly removed. The formula operators are similar in effect to the Wilkinson and Rogers notation used by such programs as Glim and Genstat. One inevitable change is that the operator ‘.’ becomes ‘:’ since the period is a valid name character in R. The notation is summarized below (based on Chambers & Hastie, 1992, p.29):

Y ~ M Y is modeled as M.

M_1 + M_2

Include M 1 and M 2.

M_1 - M_2

Include M 1 leaving out terms of M 2.

M_1 : M_2

The tensor product of M 1 and M 2. If both terms are factors, then the “subclasses” factor.

M_1 %in% M_2

Similar to M_1:M_2, but with a different coding.

M_1 * M_2 M_1 + M_2 + M_1:M_2.

M_1 / M_2 M_1 + M_2 %in% M_1.

M^n

All terms in M together with “interactions” up to order n

I(M)

Insulate M. Inside M all operators have their normal arithmetic meaning, and that term appears in the model matrix.

Note that inside the parentheses that usually enclose function arguments all operators have their normal arithmetic meaning. The function I() is an identity function used to allow terms in model formulae to be defined using arithmetic operators. Note particularly that the model formulae specify the columns of the model matrix, the specification of the parameters being implicit. This is not the case in other contexts, for example in specifying nonlinear models.

Contrasts

We need at least some idea how the model formulae specify the columns of the model matrix. This is easy if we have continuous variables, as each provides one column of the model matrix (and the intercept will provide a column of ones if included in the model). What about a k-level factor A? The answer differs for unordered and ordered factors. For unordered factors k − 1 columns are generated for the indicators of the second, . . . , kth levels of the factor.

(Thus the implicit parameterization is to contrast the response at each level with that at the first.) For ordered factors the k − 1 columns are the orthogonal polynomials on 1, . . . , k, omitting the constant term. Although the answer is already complicated, it is not the whole story. First, if the intercept is omitted in a model that contains a factor term, the first such term is encoded into k columns giving the indicators for all the levels. Second, the whole behavior can be changed by the options setting for contrasts. The default setting in R is

options(contrasts = c("contr.treatment", "contr.poly"))

The main reason for mentioning this is that R and S have different defaults for unordered factors, S using Helmert contrasts. So if you need to compare your results to those of a textbook or paper which used S-Plus, you will need to set

options(contrasts = c("contr.helmert", "contr.poly"))

This is a deliberate difference, as treatment contrasts (R’s default) are thought easier for newcomers to interpret. We have still not finished, as the contrast scheme to be used can be set for each term in the model using the functions contrasts and C. We have not yet considered interaction terms: these generate the products of the columns introduced for their component terms.

Although the details are complicated, model formulae in R will normally generate the models that an expert statistician would expect, provided that marginality is preserved. Fitting, for example, a model with an interaction but not the corresponding main effects will in general lead to surprising results, and is for experts only.

Next: Linear models

Summary: Index