The function aperm(a, perm) may be used to permute an array, a. The argument perm must be a permutation of the integers {1, . . . , k}, where k is the number of subscripts in a. The result of the function is an array of the same size as a but with old dimension given by perm[j] becoming the new j-th dimension. The easiest way to think of this operation is as a generalization of transposition for matrices. Indeed if A is a matrix, (that is, a doubly subscripted array) then B given by

> B <- aperm(A, c(2,1))

is just the transpose of A. For this special case a simpler function t() is available, so we could have used B <- t(A).

Matrix facilities

As noted above, a matrix is just an array with two subscripts. However it is such an important special case it needs a separate discussion. R contains many operators and functions that are available only for matrices. For example t(X) is the matrix transpose function, as noted above. The functions nrow(A) and ncol(A) give the number of rows and columns in the matrix A respectively.

Matrix multiplication

The operator %*% is used for matrix multiplication. An n by 1 or 1 by n matrix may of course be used as an n-vector if in the context such is appropriate. Conversely, vectors which occur in matrix multiplication expressions are automatically promoted either to row or column vectors, whichever is multiplicatively coherent, if possible, (although this is not always unambiguously possible, as we see later). If, for example, A and B are square matrices of the same size, then

> A * B

is the matrix of element by element products and

> A %*% B

is the matrix product. If x is a vector, then

> x %*% A %*% x

is a quadratic form.[1]

The function crossprod() forms “crossproducts”, meaning that crossprod(X, y) is the same as t(X) %*% y but the operation is more efficient. If the second argument to crossprod() is omitted it is taken to be the same as the first. The meaning of diag() depends on its argument. diag(v), where v is a vector, gives a diagonal matrix with elements of the vector as the diagonal entries. On the other hand diag(M), where M is a matrix, gives the vector of main diagonal entries of M. This is the same convention as that used for diag() in Matlab. Also, somewhat confusingly, if k is a single numeric value then diag(k) is the k by k identity matrix!

Linear equations and inversion

Solving linear equations is the inverse of matrix multiplication. When after > b <- A %*% x only A and b are given, the vector x is the solution of that linear equation system. In R, > solve(A,b) solves the system, returning x (up to some accuracy loss). Note that in linear algebra, formally x = A−1b where A−1 denotes the inverse of A, which can be computed by solve(A) but rarely is needed. Numerically, it is both inefficient and potentially unstable to compute x <- solve(A) %*% b instead of solve(A,b).

The quadratic form x0A−1x which is used in multivariate computations, should be computed by something like[2] x %*% solve(A,x), rather than computing the inverse of A.

Eigenvalues and eigenvectors

The function eigen(Sm) calculates the eigenvalues and eigenvectors of a symmetric matrix Sm. The result of this function is a list of two components named values and vectors. The assignment

> ev <- eigen(Sm)

will assign this list to ev. Then ev$val is the vector of eigenvalues of Sm and ev$vec is the matrix of corresponding eigenvectors. Had we only needed the eigenvalues we could have used the assignment:

> evals <- eigen(Sm)$values

evals now holds the vector of eigenvalues and the second component is discarded. If the expression

> eigen(Sm)

is used by itself as a command the two components are printed, with their names. For large matrices it is better to avoid computing the eigenvectors if they are not needed by using the expression

> evals <- eigen(Sm, only.values = TRUE)$values

Singular value decomposition and determinants

The function svd(M) takes an arbitrary matrix argument, M, and calculates the singular value decomposition of M. This consists of a matrix of orthonormal columns U with the same column space as M, a second matrix of orthonormal columns V whose column space is the row space of M and a diagonal matrix of positive entries D such that M = U %*% D %*% t(V). D is actually returned as a vector of the diagonal elements. The result of svd(M) is actually a list of three components named d, u and v, with evident meanings. If M is in fact square, then, it is not hard to see that

> absdetM <- prod(svd(M)$d)

calculates the absolute value of the determinant of M. If this calculation were needed often with a variety of matrices it could be defined as an R function

> absdet <- function(M) prod(svd(M)$d)

after which we could use absdet() as just another R function. As a further trivial but potentially useful example, you might like to consider writing a function, say tr(), to calculate the trace of a square matrix. [Hint: You will not need to use an explicit loop. Look again at the diag() function.] R has a builtin function det to calculate a determinant, including the sign, and another, determinant, to give the sign and modulus (optionally on log scale).

Least squares fitting and the QR decomposition

The function lsfit() returns a list giving results of a least squares fitting procedure. An assignment such as

> ans <- lsfit(X, y)

gives the results of a least squares fit where y is the vector of observations and X is the design matrix. See the help facility for more details, and also for the follow-up function ls.diag() for, among other things, regression diagnostics. Note that a grand mean term is automatically included and need not be included explicitly as a column of X. Further note that you almost always will prefer using lm(.) to lsfit() for regression modelling.

Another closely related function is qr() and its allies. Consider the following assignments

These compute the orthogonal projection of y onto the range of X in fit, the projection onto the orthogonal complement in res and the coefficient vector for the projection in b, that is, b is essentially the result of the Matlab ‘backslash’ operator. It is not assumed that X has full column rank. Redundancies will be discovered and removed as they are found. This alternative is the older, low-level way to perform least squares calculations. Although still useful in some contexts, it would now generally be replaced by the statistical models features.

Forming partitioned matrices, cbind() and rbind()

As we have already seen informally, matrices can be built up from other vectors and matrices by the functions cbind() and rbind(). Roughly cbind() forms matrices by binding together matrices horizontally, or column-wise, and rbind() vertically, or row-wise. In the assignment

> X <- cbind(arg_1, arg_2, arg_3, ...)

the arguments to cbind() must be either vectors of any length, or matrices with the same column size, that is the same number of rows. The result is a matrix with the concatenated arguments arg 1, arg 2, . . . forming the columns. If some of the arguments to cbind() are vectors they may be shorter than the column size of any matrices present, in which case they are cyclically extended to match the matrix column size (or the length of the longest vector if no matrices are given). The function rbind() does the corresponding operation for rows. In this case any vector argument, possibly cyclically extended, are of course taken as row vectors. Suppose X1 and X2 have the same number of rows. To combine these by columns into a matrix X, together with an initial column of 1s we can use

> X <- cbind(1, X1, X2)

The result of rbind() or cbind() always has matrix status. Hence cbind(x) and rbind(x) are possibly the simplest ways explicitly to allow the vector x to be treated as a column or row matrix respectively.

The concatenation function, c(), with arrays

It should be noted that whereas cbind() and rbind() are concatenation functions that respect dim attributes, the basic c() function does not, but rather clears numeric objects of all dim and dimnames attributes. This is occasionally useful in its own right. The official way to coerce an array back to a simple vector object is to use as.vector()

> vec <- as.vector(X)

However a similar result can be achieved by using c() with just one argument, simply for this side-effect:

> vec <- c(X)

There are slight differences between the two, but ultimately the choice between them is largely a matter of style (with the former being preferable).

Frequency tables from factors

Recall that a factor defines a partition into groups. Similarly a pair of factors defines a two way cross classification, and so on. The function table() allows frequency tables to be calculated from equal length factors. If there are k factor arguments, the result is a k-way array of frequencies.

Suppose, for example, that statef is a factor giving the state code for each entry in a data vector. The assignment

> statefr <- table(statef)

gives in statefr a table of frequencies of each state in the sample. The frequencies are ordered and labelled by the levels attribute of the factor. This simple case is equivalent to, but more convenient than,

> statefr <- tapply(statef, statef, length)

Further suppose that incomef is a factor giving a suitably defined “income class” for each entry in the data vector, for example with the cut() function:

> factor(cut(incomes, breaks = 35+10*(0:7))) -> incomef

Then to calculate a two-way table of frequencies:

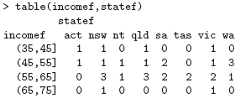
Extension to higher-way frequency tables is immediate.

Next: Lists and data frames

Summary: Index