The "General Heston Model" is:

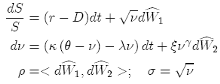
Using X1 = S, and X2 = ν, the previous equation can be transformed to a vector with independent noise sources:

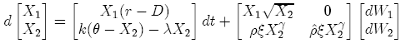
to obtain the corresponding general form:

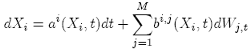
where:

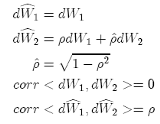
Using the definition for the Milstein scheme, the approximation of X has the following form:

(52)

f or i = 1, ..., N ; j = 1, ..., M

where:

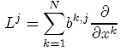
Substituting:

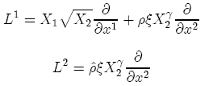
Then:

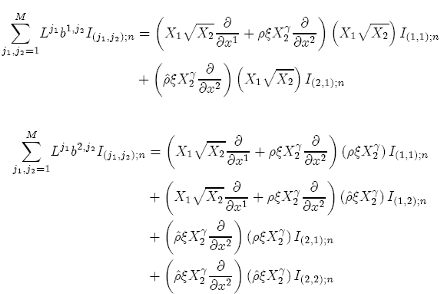
Calculating the respective derivatives, we get:

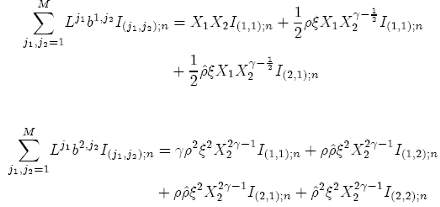
The double integrals have the following properties:

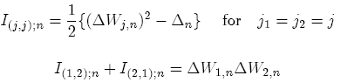
Substituting the previous properties, we get:

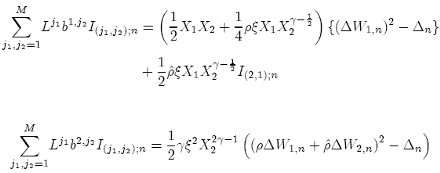
Substituting the previous results in {52}, we get:

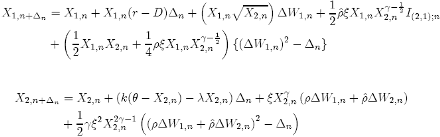
Finally, returning to the original variables and the correlated noise, we get:

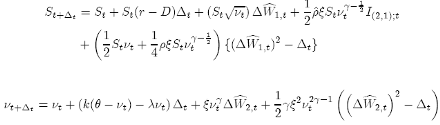
where:

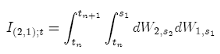
Prof. Klaus Schmitz

Next: Numerical Data of the Double Integral

Summary: Index