We shall say that an approximation process Y converges in the strong sense with order γ ε (0, ∞] with a continuous process X if there exists a finite constant K and a positive constant δ0 such that:

for any time discretization of T with maximum step size δ ε (0, δ0).

In this section, we present the strong stochastic Taylor schemes of orders 0.5, 1.0 and 1.5 for the N-dimensional Ito SDE with an M-dimensional Wiener process {3} as well as the strong order 2.0 stochastic Taylor scheme for the corresponding Stratonovich SDE.

Euler scheme

The strong stochastic Taylor scheme of order 0.5 for the {SDE-3}, usually called the stochastic Euler scheme, has the component-wise form:

(9)

f or i = 1, ..., N ; j = 1, ..., M

where ∆n = tn+1 − tn is the length of the nth time step and ∆W^jn = W^jn+1 −W^jn is the N(0, ∆n)−distributed increment of the jth component of the M-dimensional standard Wiener process Wt on the discretization subinterval [tn, tn+1]. Here ∆W ^j1 n and ∆W ^j2 n are independent for j1 ? j2.

Milstein scheme

The strong stochastic Taylor scheme of order 1.0 for the {SDE-3}, usually called the Milstein scheme, has the component-wise form:

(10)

f or i = 1, ..., N ; j = 1, ..., M

where I(j1,j2);n is the multiple Ito integral:

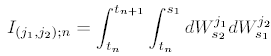
These double integrals have the following properties:

(11)

for: j1 ≠ j2.

Prof. Klaus Schmitz

Next: Milstein scheme for commutative noise

Summary: Index