The double integrals have the following main property:

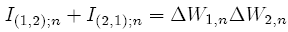(27)

and if we simulate the two integrals using the subdivision method from Kloeden described above, we can see that this is only true in the first time step (n = 1). Furthermore, if we calculate the variance of the integral, we can conclude that it depends on the time step n.

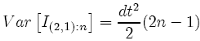
The variance of the integral change as the time step n increases (figure 2.2), tends to zero when n and NK tend to infinity:

Var [I(2,1):n]= 0 if n --> ∞ and NK -->∞

However, if we change the initial conditions {26} to zero, the variance of the integral changes to:

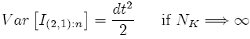
for all n time steps; that is, exactly half of the variance of ∆W_1,n∆W_2,n. Indeed, if we test the main property {27}, we can see that it is true for all time steps n, and the variance of the integral does not change for all n (figure 2.2).

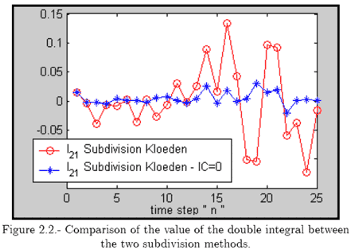
Furthermore, if we simulate both methods with different integration steps Nk, and if:

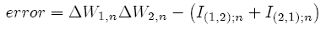
we have to see that this error tends to zero as Nk tends to infinity. This behavior is not true in the first method (figure 2.3).

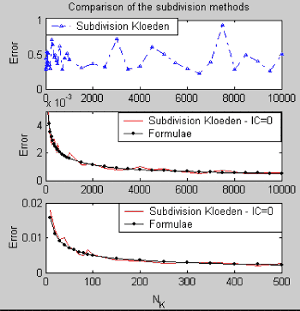
Figure 2.3.- Comparison of the maxim error of 100 simulations between the two subdivision methods with different integration step NK .

In summary, we conclude that the double Ito integral {24} can be simulated using the subdivision method given by Kloeden by changing the initial conditions {26} to zero. The accuracy or error in the calculation of {24} depends directly on the value of "NK" and is given by the next approximation formulae (figure 2.3):

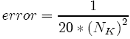(28)

Prof. Klaus Schmitz

Next: Fourier Lévy formulae

Summary: Index