Certain structural relationships between the noise coefficient vectors bj,j of an SDE that are known as commutative noise allow considerable simplifications to numerical schemes, in particular, the avoidance of the need to simulate multiple stochastic integrals. The {SDE-3} is said to have commutative noise (of the first kind) when:

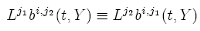
for: i = 1, ..., N ; j1, j2 = 1, ..., M

Then the identities {11} for j1, j2 = 1, ..., M with j1 ≠ j2 can be used to simplify the Milstein scheme to give:

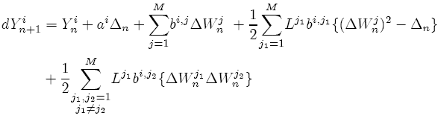(12)

which is called the Milstein scheme for commutative noise.

Order 1.5 strong stochastic Taylor scheme

The i th component of the order 1.5 strong Taylor scheme for the Ito {SDE- 3} is given by:

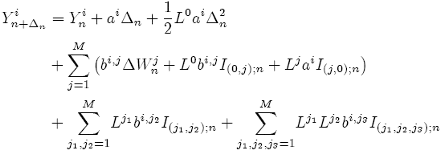(13)

for i = 1, ..., N, where I(j1,j2,j3);n is the multiple Ito integral:

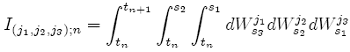
with the special case:

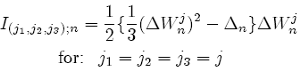
Also

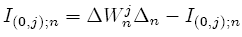
where the random variable

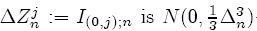
distributed and has covariance

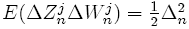
Order 2.0 strong stochastic Taylor scheme

The order 2.0 strong Taylor scheme for the N-dimensional Stratonovich {SDE-5} with an M-dimensional Wiener process:

f or i = 1, ..., N ; j = 1, ..., M

is given by:

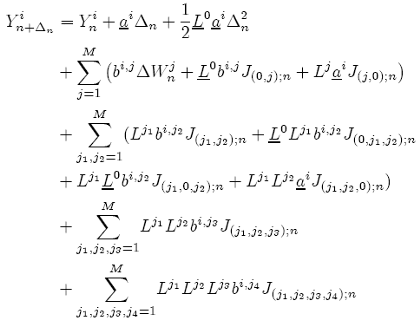(14)

for i = 1, ..., N. The J(j1,j2);n, J(j1,j2,j3);n and J(j1,j2,j3,j4);n expressions here denote the corresponding Stratonovich integrals with respect to the components of the given Wiener process.

Prof. Klaus Schmitz

Next: Approximations of Volatility Models

Summary: Index