Una delle applicazioni più importanti delle reti neurali è sicuramente quella delle previsioni di fenomeni complessi come i fenomeni meteorologici o quelli finanziari o socio-economici. Esistono metodi per la previsione di tali fenomeni che si basano su tre diverse linee di principio:
1) classico
2) frequenziale
3) moderno
Non vogliamo analizzare in questa sede queste tre teorie, ma accennare solo alla seconda che si basa sulla scomposizione in componenti armoniche secondo la legge di Fourier. Il principale difetto di questo metodo è che i calcoli relativi alle componenti frequenziali più alte appesantiscono eccessivamente l'algoritmo al punto che si rende necessario accontentarsi di selezionare le armoniche che si ritengono maggiormente influenti, ottenendo un evidente errore di approssimazione.
Con una rete neurale è possibile fare previsioni analizzando le serie storiche dei dati esattamente come con questi sistemi ma non è necessario fare supposizione alcuna per restringere il problema ne, tanto meno, applicare la trasformata di Fourier. un difetto comune ai metodi di analisi sopra elencati è quello di essere applicabili solamente se si attuano delle restrizioni nel problema utilizzando delle ipotesi che talvolta potrebbero rivelarsi errate. In pratica si addestra la rete neurale con successioni di serie storiche di dati del fenomeno che si vuole prevedere.
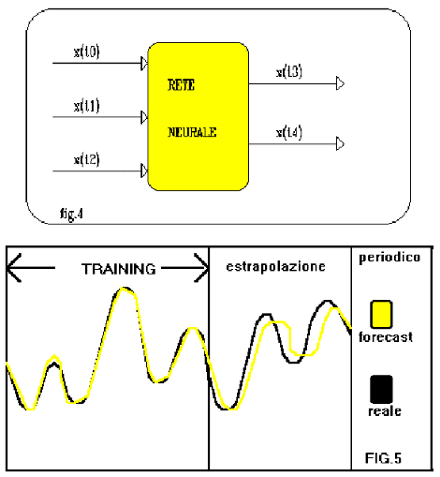
Supponiamo di voler prevedere, sulla base di n valori consecutivi che la variabile x(t) ha assunto, i successivi m valori che assumerà: addestriamo la rete di fig.4 con la prima serie storica di n dati della variabile in input e la seconda serie di successivi m dati in output e cosi via per altre coppie di serie storiche ciascuna delle quali rappresenta un esempio.
In questo modo la rete apprende l'associazione che esiste tra i valori della variabile in n punti e quelli in m punti successivi ma anche l' associazione tra le derivate in quanto l'informazione di due soli valori vicini della variabile è un indice della derivata in quel punto. Esistono due tipi di previsione: univariata e multivariata. La prima riguarda la previsione dei valori di una sola variabile di un fenomeno in base ai dati storici della variabile stessa. La seconda riguarda la previsione dei valori di più variabili in base ai dati storici delle stesse ed eventualmente anche di altre variabili: in questo secondo caso è l'insieme dei valori delle sequenze storiche di tutte le variabili di input che concorre alla determinazione dell'output di ognuna delle variabili su cui si vuole fare la previsione
. Esistono casi in cui le sequenze storiche elementari(quelle che rappresentano un esempio) devono essere composte da molti dati consecutivi per avere dei buoni risultati e ciò comporta la necessità di utilizzare reti con un numero di inputs molto elevato: è possibile fare questo ma, talvolta, si preferisce utilizzare "reti ricorrenti" che sono reti neurali dotate di "memorie sugli input" tali che ogni variabile possa avere un solo input fisico ma la rete ad ogni istante t sia condizionata non solo dagli input dell’ istante t ma anche da quelli degli istanti precedenti(t-1 ... t-n , dove n rappresenta l'ampiezza delle sequenze storiche).
Luca Marchese
Successivo: Previsione Univariata
Sommario: Indice