Si tratta in pratica di ciò di cui si è gia parlato riferendoci alla fig.4. Vediamo due esempi di previsione di due processi dei quali il primo è di tipo periodico(naturalmente la previsione di un processo periodico ha senso solo a livello didattico), e il secondo aperiodico. Possiamo effettuare previsioni sulla funzione:

x(t)=sin(2*pigreco*t/40)+sin(2*pigreco*t/100) [due sinusoidi con periodi 40 e 100]

Utilizziamo il generatore di file di esempi sin_gen e addestriamo una rete neurale error_back_propagation con il file di esempi generato. Usiamo una rete neurale con 2 inputs che corrispondono ad una serie storica di 2 valori e con 1 solo output che corrisponde al valore successivo previsto: con un training set di 40 esempi(120 valori del file period.lrn composto di 200 valori) e periodo 40 (la seconda sinusoide assume automaticamente periodo 100), otteniamo il risultato di fig.5 (il target_error=0.01. E stato ottenuto con un numero considerevole di epoche su una spark station).

Il risultato viene ottenuto ripetendo piu volte la funzione exec del programma di simulazione di rete neurale con valori di input scelti nel range dei valori possibili della funzione Utilizzando una rete con due input e un output abbiamo una informazione su due valori precedenti ma anche sulla derivata in quel punto.

Per effettuare l'addestramento con con il programma presentato nel capitolo precedente si può utilizzare lo stesso training set impostando diversamente il numero degli input e degli output(tenendo presente che deve essere (n_in + n_out)*n_es < n_gen). Avendo il programma utilizzato una funzione di trasferimento a sigmoide che fornisce valori compresi tra 0 e 1, il programma sin_gen genera degli esempi normalizzati con valori che variano tra 0.0 e 1.0.

NOTA IMPORTANTE: bisogna distinguere le previsioni fatte nel range del training set(interpolazioni), che non sono previsioni vere e proprie, da quelle effettuate al di fuori di esso che rappresentano la reale capacità predittiva della rete neurale.

IN PRATICA: nella previsione di fenomeni complessi si utilizzano serie storiche composte da un numero molto maggiore di dati e i valori da predire sono sempre più di uno a seconda del campo predittivo che l'applicazione richiede.

Passiamo adesso ad analizzare una funzione aperiodica che risulta essere sicuramente più interessante ai fini delle previsioni. Utilizziamo una funzione composta dalla sovrapposizione di due sinusoidi di cui una con periodo incommensurabile:

x(t)=sin(2*pigreco*t/40)+sin(sqrt(2*pigreco*t/40))

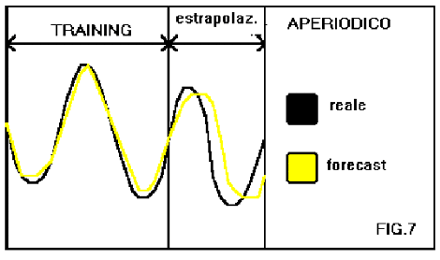
Generiamo il file di esempi con il generatore sin_gen selezionando la funzione 2 e addestriamo una rete con tre inputs e un output(usiamo 5 neuroni in ogni strato hidden). Il risultato di previsione che otteniamo dopo un addestramento che porta ad un errore=0.01 è quello di fig.7. L'addestramento è stato effettuato con 16 esempi che costituiscono 64 generazioni (16*(3input+1output)) delle 100 generate da sin_gen utilizzando l'opzione aperiodica e periodo=40.

Adesso proviamo a verificare se la rete addestrata con il processo aperiodico è in grado di fare predizioni anche sulle componenti frequenziali del processo stesso. Possiamo generare con sin_gen due files di riferimento con i valori reali delle componenti frequenziali e prelevare da essi delle serie storiche di tre dati consecutivi da usare come input della funzione exec e costruire la funzione in base al valore dato come output nel file net.out.

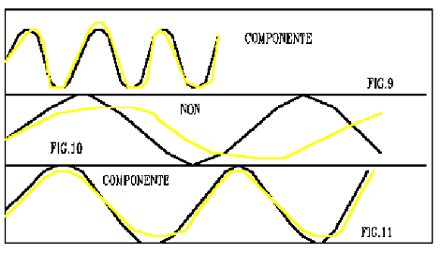
Sia nel caso della prima componente che nel caso della seconda abbiamo risultati di previsione analoghi a quelli della funzione composta e ne deduciamo che la rete è in grado di riconoscere le componenti frequenziali del processo, proprio come se applicasse una trasformata di Fourier "virtuale". Per avere una controprova di ciò possiamo tentare di fare una previsione su una sinusoide di frequenza differente da quelle componenti: la rete fa delle previsioni con errori tangibilmente maggiori dimostrando di essere sensibile solamente alle componenti frequenziali del processo relativo ai dati di addestramento(fig.9 fig.10 fig.11).

Effettivamente questa controprova risulta molto più evidente se l'addestramento avviene con serie storiche più ampie di quella utilizzata, attraverso le quali la rete assume informazioni più precise in merito alla frequenza delle varie componenti.

Luca Marchese

Successivo: Processi non stazionari

Sommario: Indice