Le opzioni finanziarie sono strumenti derivati che danno a chi le possiede la facoltà di acquistare (call) o vendere (put) alla, o entro, la data di scadenza un certo quantitativo dell’attività sottostante ad un certo prezzo, detto prezzo d’esercizio. Mentre a scadenza il valore dell’opzione si ricava confrontando il prezzo del sottostante con il prezzo d’esercizio, durante la vita dell’opzione questo può essere visto come funzione del prezzo del bene sottostante St, del prezzo d’esercizio e del tempo mancante alla scadenza ( τ=Tt). Per un'opzione call avremo cioè:
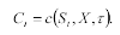
Nella teoria del prezzaggio di opzioni è di fondamentale importanza lo studio di Black e Scholes. I due Autori, sulla base di determinate “condizioni ideali”, riuscirono a derivare un’espressione in forma chiusa per determinare il prezzo di una call europea su di un’azione. Le ipotesi del modello sono:
• l’opzione è una call di tipo europeo;
• il bene sottostante non paga dividendi;
• il tasso d’interesse a breve termine è noto e costante per tutta la durata dell’opzione;
• non si considerano costi di transazione;
• si può dare e prendere a prestito illimitatamente ed allo stesso tasso d’interesse a breve termine;
• si può operare allo scoperto;
• il prezzo del bene sottostante si evolve in modo continuo secondo il seguente andamento diffusivo
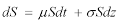
dove:
S: prezzo del bene sottostante al tempo corrente,
t: tempo,
dz: è la variazione di un particolare processo di Markov, noto come processo di Wiener
µ: rendimento istantaneo atteso del bene sottostante,
σ: scarto quadratico medio (volatilità) del rendimento istantaneo del bene sottostante.
Quest’ultima ipotesi sulla dinamica del prezzo dell’attività sottostante è particolarmente importante, in quanto implica che, a scadenza, il prezzo del bene sottostante segua una distribuzione di probabilità di tipo log-normale e, di conseguenza, che i rendimenti istantanei si distribuiscono normalmente con varianza costante nel tempo. Le opzioni oggetto del nostro studio considerano come bene sottostante un particolare indice rappresentativo del mercato azionario inglese: l’indice FTSE-100.
Essendo un indice azionario una somma pesata di più azioni, la formula per la valutazione di tali opzioni non presenta grandi differenze rispetto alla soluzione originaria di B-S. La principale complicazione è data dal fatto che le azioni che compongono l’indice possono distribuire dei dividendi durante la vita dell’opzione, e dal fatto che la maggior parte degli indici non vengono corretti al fine di considerare questo fenomeno.
L’introduzione del tasso di dividendo 6 comporta, per il titolo che ne prevede la distribuzione, un tasso di crescita minore rispetto ad un titolo che non distribuisce dividendi 7. Il valore corrente del titolo va, quindi, ridotto nel modo seguente:
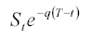
dove q è il tasso continuo di dividendo (dividend yield). Il valore dell’opzione call nel caso il titolo sottostante paghi un tasso di dividendo continuo nel tempo pari a q, parametro supposto noto e costante sarà quindi:
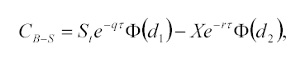
con
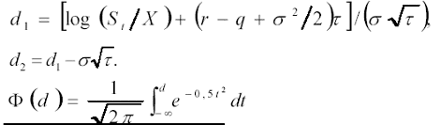
Tali risultati sono stati ottenuti per la prima volta da Merton. Gli input del modello di Black e Scholes per la valutazione di opzioni su indici azionari sono quindi:
• il prezzo del bene sottostante (nel nostro caso l’indice azionario -FTSE-100),
• il prezzo d’esercizio,
• il tempo mancante a scadenza,
• il tasso d’interesse privo di rischio utilizzato,
• il tasso di dividendo (dividend yield),
• la volatilità.
Le prime tre variabili si possono ricavare facilmente dalla lettura dei quotidiani finanziari. Per quanto riguarda la stima il tasso d’interesse il modello B-S ipotizza che ciascun soggetto possa dare e prendere a prestito illimitatamente al tasso privo di rischio, supposto noto e costante per la durata residua dell’opzione. Nella realtà, il tasso d’interesse tende a variare e ad assumere, generalmente, valori diversi a seconda che si chieda o dia a prestito denaro.
I dati sui tassi d’interesse utilizzati al fine di ottenere una buona stima di tale parametro sono i seguenti tassi interbancari: tasso a brevissimo termine (una settimana), tassi a 1, 3, 6, 12 mesi. Il tasso d’interesse che si accorda con il tempo a scadenza di ciascuna opzione viene ottenuto interpolando linearmente i due tassi interbancari più vicini. Si ritiene, in questo modo, di approssimare in modo ottimale il tasso d’interesse privo di rischio secondo quanto ipotizzato da B-S. Il tasso di dividendo (dividend yield) si può ricavare presso il sito internet della borsa londinese che ne fornisce, inoltre, una serie storica. Nel nostro lavoro considereremo tale parametro costante, non solo per tutta la vita residua della singola opzione, ma anche per tutto il periodo considerato e quindi per tutte le opzioni valutate.
La stima della volatilità è ottenuta implicitamente dai prezzi di mercato delle opzioni. In particolare, è stata effettuata una media semplice delle volatilità implicite legate alle due opzioni i cui prezzi di esercizio sono più vicini al prezzo del bene sottostante, data una certa scadenza. L’utilizzo di una media ha lo scopo di mitigare la presenza di eventuali errori nei prezzi delle opzioni e di minimizzare l’effetto di dati “rumorosi”. Nel caso in cui nello stesso giorno siano quotate opzioni con scadenze diverse, si provvederà ad effettuare un’ulteriore media semplice delle volatilità implicite ottenute con l’operazione precedente. L’utilizzo di tale sistema di pesi per la stima della volatilità non deriva da un’analisi rigorosa dei dati oggetto di studio, ma si basa sulle seguenti osservazioni:
• le opzioni at-the-money sono, generalmente, le più scambiate, e quindi la volatilità implicita collegata ha contenuto informativo più attendibile,
• i prezzi delle opzioni at-the-money 8 sono più sensibili al cambiamento nella volatilità e quindi, a parità di altre condizioni, un’errata misurazione della volatilità provoca errori più consistenti per tale categoria di opzioni.
6L’introduzione dei dividendi nella formula di B-S può avvenire in due modi, a seconda che il loro pagamento sia considerato discreto, avvenga cioè a date precise, oppure continuo, secondo un determinato tasso.
7 Ricordiamo che i dividendi vengono distribuiti ai possessori delle azioni della società e non ai possessori delle opzioni su tali azioni. Nella valutazione bisogna quindi considerare la possibilità che durante la vita dell’opzione vengano distribuiti dividendi.
8 Un’opzione è detta “in-the-money” se il suo esercizio immediato genera un flusso di cassa positivo, altrimenti è detta “out-of-the-money”. Nel caso in cui il prezzo d’esercizio sia pari al prezzo del bene sottostante l’opzione è detta “at-the-money”.
M.Billio, M. Corazza, M. Gobbo
Successivo:Modelli switching regime: valutazione dell'opzione
Sommario: Indice