In questo paragrafo caratterizziamo il livello di reddito pro-capite che prevale nell’equilibrio di
lungo periodo del modello appena proposto. Prima, però, partiamo con una definizione formale di balanced growth path equilibrium (BGPE), o equilibrio (dinamico) di steady-state:
Definizione: Balanced Growth Path Equilibrium (BGPE) o equilibrio (dinamico) di
steady state
Definiamo equilibrio di crescita bilanciata (balanced growth path equilibrium), o di steady-state dinamico, una situazione nella quale tutte le variabili di stato crescono a saggio costante positivo.Nel modello che stiamo esaminando le variabili di stato sono il capitale fisico ed umano (entrambi misurati in termini pro-capite, k e h rispettivamente). Applicando la definizione di balanced growth path equilibrium all’equazione (5) troviamo che nell’equilibrio di lungo periodo (steady-state dinamico) ciascun individuo allocherà una frazione costante del proprio stock di capitale umano alla produzione dell’omogeneo bene di consumo finale e alla produzione di nuovo capitale umano ( ubp è costante, trattandosi del valore di steady-state di u ). Viceversa, mettendo insieme le equazioni (4) e (3) con la definizione di balanced growth path equilibrium otteniamo che nel lungo periodo deve essere vera la seguente relazione (per ragioni di semplificazione formale, d’ora in poi non riportiamo più il pedice t accanto alle variabili che dipendono dal tempo):
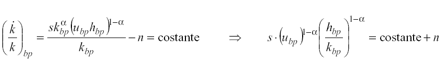 (6)
(6)
dove anche in questo caso abbiamo indicato con “bp” il valore di equilibrio della variabile in oggetto. Con s e n esogenamente dati e ubp costante, dall’equazione (6) è possibile trarre due importanti conclusioni per quanto concerne l’equilibrio di lungo periodo:
(6a) h e k crescono in steady-state allo stesso saggio costante,[9] dato da: gbp = 1-ubp;
(6b) 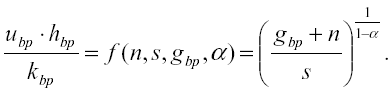
Dall’equazione (3), e tenuto conto che in equilibrio
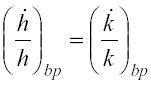
e ubpè costante, è agevole ricavare:
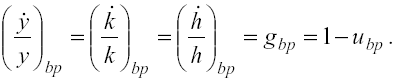 (7)
(7)
L’equazione (7) suggerisce che lungo il sentiero di crescita bilanciata reddito, capitale fisico e
capitale umano (tutti misurati in termini pro-capite) crescono allo stesso tasso costante (che è una funzione lineare di u ).A questo punto, per determinare il livello di equilibrio del reddito pro-capite, abbiamo prima di tutto bisogno di trovare il livello di equilibrio del capitale fisico pro-capite ( Kbp ). A questo scopo, riconsideriamo l’equazione (6) di cui sopra (sapendo che il tasso di crescita di k è pari a gbp in steadystate), ottenendo la seguente equazione per Kbp :
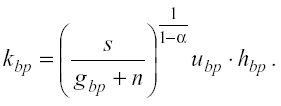 (8)
(8)
Dato Kbp , il livello di reddito pro-capite di equilibrio (Ybp ), dall’equazione (3) sarà invece pari a:
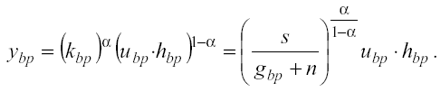 (9)
(9)
9 Il fatto che h e k crescano allo stesso saggio costante equivale ad affermare che il loro rapporto è anch’esso costante (in equilibrio capitale umano e fisico sono tra loro complementari). L’ipotesi di complementarietà tra questi due fattori produttivi è oggi ampiamente usata dal punto di vista teorico ed accettata da quello empirico (si veda al riguardo J. Mincer, 1996 per una breve rassegna sull’argomento).
Nel modello abbiamo tre variabili endogene:
1) il rapporto di equilibrio tra le due variabili di stato
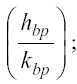
2) la frazione di capitale umano che ogni individuo destina ad attività produttive nel lungo periodo (ubp), e infine
3) il tasso di crescita dell’economia in steady-state (gbp). Per determinare ubp imponiamo la seguente condizione di arbitraggio (arbitrage condition, d’ora in avanti AC):
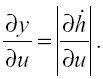
Per comprendere il significato intuitivo della (AC), si ricordi che nel modello la variabile di scelta dell’agente rappresentativo è rappresentata da u (la frazione del proprio stock di capitale umano che egli decide di allocare ad attività produttive).
Una volta determinato il valore di equilibrio di u (ubp), sarà automaticamente determinata anche la frazione di capitale umano che in equilibrio verrà destinata all’accumulazione di skills (1- ubp-) , e dunque il tasso di crescita di steady-state del sistema economico (gbp). Ciò che la (AC) dice è semplicemente che il medesimo agente rappresentativo avrà interesse a
modificare u fino al punto in cui la variazione di output finale (pari a ∂y ) che egli può ottenere da una variazione marginale di u (pari a ∂u) è precisamente uguale alla variazione (di segno opposto) nell’accumulazione di capitale umano (∂h) derivante dalla medesima variazione in u .
Quando questa condizione viene soddisfatta (cioè in equilibrio), egli non avrà più alcun incentivo a variare ulteriormente u (e quindi ubp sarà costante). Dal momento che u entra con segno positivo nella produzione dell’output finale e negativo in quella di capitale umano, ciò spiega perché nella (AC) prendiamo il valore assoluto della quantità a destra del segno di uguale. In altri termini, la condizione di arbitraggio equivale ad imporre che in equilibrio l’ultima unità di tempo a disposizione dell’agente abbia (in valore assoluto) la stessa produttività a prescindere dal fatto che essa venga allocata alla produzione del bene finale ovvero all’accumulazione di skills. Dato ciò, dalle equazioni (3) e (5) e ricordando che la (AC) è una condizione di equilibrio di lungo periodo (ovvero vale solo nello steady-state), si ottiene che
deve essere soddisfatta la seguente equazione:
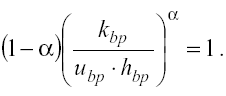 (10)
(10)
Abbiamo ora tre incognite ( hbp / , kbp ubpe gbp ) in tre equazioni ((6b), (7) e (10)) che, risolte
simultaneamente, danno:
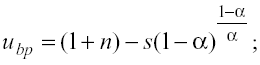 (11)
(11)
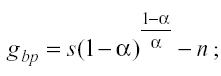 (12)
(12)
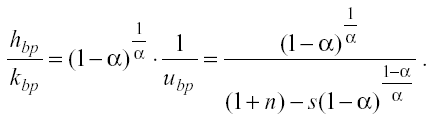 (13)
(13)
Dalle equazioni (11), (12) e (13) è immediato notare che deve essere soddisfatta la seguente restrizione sui parametri:
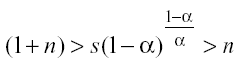 (14)
(14)
affinché sia simultaneamente vero che
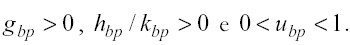
Si noti, infine, che nell’equilibrio di steady-state u , g e k h / risultano unicamente funzione dei
parametri esogeni del modello (α, s ed n ). In altri termini queste tre variabili, pur essendo
endogenamente determinate, risultano completamente insensibili a variazioni di policy.[10] In Appendice A, usando un diagramma di fase, studiamo la dinamica del modello e forniamo un’analisi grafica della definizione di balanced growth path equilibrium (o equilibrio di steady-state) finora utilizzata. Nel prossimo paragrafo, invece, calcoliamo il segno della relazione che lega le tre endogene del modello con la propensione marginale al risparmio ( s ), il tasso di crescita della popolazione ( n ) e la quota del reddito che va al capitale (α).
Documento del Prof. Alberto Bucci e del Prof. Daniele Checchi
Successivo: Analisi di statica comparata.
Sommario: Indice