Al fine di eseguire un test di regressione per verificare la presenza di mispricing nei residui, bisogna definire delle quantità strumentali alla costruzione del test medesimo. Queste quantità sono l’”holding period return”, l’”expected holding period return” e l’”abnormal return”. Se indichiamo ancora con Φ_t il set di parametri del modello stimati all’istante temporale t, e indichiamo con Xce(Φ_t) il prezzo stimato e con Xc°(t, T) il prezzo osservato in t, allora possiamo dare le seguenti definizioni:

· Holding period return (del titolo i-simo):

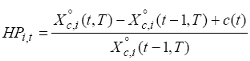(1.3.1a)

se t è misurato in giorni, allora questo sarà un HPi,t giornaliero ( c(t) = cedola eventualmente pagata dal coupon bond in t).

· Expected holding period return (del titolo i-simo):

(1.3.1b)

tale equazione fornisce una misura del rendimento equo, atteso, dell’investimento, ovvero il rendimento che si otterrebbe dal mercato se questo fosse in equilibrio, in base alle indicazioni del modello CIR; in sostanza, tale quantità esprime un rendimento che tiene conto dei movimenti attesi del mercato: è un rendimento che “cattura i movimenti di mercato”.

· Abnormal return (del titolo i-esimo):

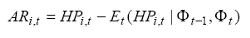(1.3.1c)

quest’ultima equazione mette evidenza come l’eliminazione dal rendimento “grezzo” HPi,t di quella quota di rendimento “diffusa” (normale), tipica del mercato (rendimento connesso al movimento di mercato), porta ad isolare quella componente del rendimento di un investimento connessa con le caratteristiche peculiari del titolo (stato di sopravvalutazione e sottovalutazione) e sulle quali si può agire per ottenere guadagni extra rispetto a quelli che fornirebbe un investimento che replica sostanzialmente l’andamento del mercato.

Fulvio Pegoraro

Successivo: Test di regressione

Sommario: Indice