Per verificare se nel residuo (differenza tra prezzo osservato e prezzo equo) generato dal modello CIR esiste una componente genuina di mispricing costruiamo il seguente test di regressione, concentrandoci innanzitutto sul brevissimo periodo (trading giornaliero): regrediamo l’ARi,t di un titolo (i-simo) maturato tra l’istante t-1 e t sul residuo percentuale osservato in t-1. Tale regressione ha, quindi, la seguente forma:

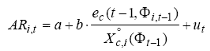(1.3.2a)

dove ARi,t è la quantità definita dalla (1.3.1c), ovvero il rendimento in eccesso rispetto a quello di mercato, e dove ut è un white noise gaussiano.

Eseguita la regressione, la risposta alla domanda d’esordio di tale sezione è data dal valore assunto dal coefficiente b (parametro economicamente rilevante). Possiamo individuare 3 casi:

· Se b = 0 e a = 0, il residuo che si forma all’istante t-1 è totalmente non informativo sul mispricing da sfruttare all’istante t, e ciò può essere dovuto o ad una sostanziale inesistenza di mispricing (effetto distorsivo del fattore econometrico) o perché i tempi di reazione del mercato sono più lunghi di un giorno (il trader ha chiuso la propria posizione troppo presto).

· Se b = -1, abbiamo la situazione diametralmente opposta, ovvero il residuo in t-1 è totalmente informativo per il trading aperto in t-1 e chiuso in t; se in t-1 osserviamo un residuo negativo (titolo sottovalutato) e tale informazione è corretta, allora il titolo acquistato in t-1 a Xc°(t-1) verrà venduto in t ad un prezzo Xc°(t) più alto per effetto dell’aggiustamento al rialzo verso il prezzo equo (l’aumento di domanda del titolo, in quanto sottovalutato, provoca un aumento del prezzo che va ad eliminare la situazione di mispricing riportando l'equilibrio) con il conseguente ottenimento di un ARi,t positivo. E’ evidente, quindi, che una relazione economicamente significativa tra il residuo e l’extra-rendimento da trading viene sancito da un parametro b negativo; se b = -1, abbiamo una situazione “ideale” di perfetta informazione sul mispricing ad un giorno.

· Se –1< b < 0, allora stiamo considerando la situazione realistica che vede il residuo non fornire sempre informazione corrette sul mispricing, ovvero stiamo osservando la situazione nella quale una quota del residuo è prodotta da stime non ottimali; tuttavia, si tenga presente che una causa di tale risultato può derivare dal fatto che il mercato necessita di più di un giorno per maturare ed eliminare il margine di arbitraggio.

Proprio per verificare questa eventuale lentezza del mercato nel riguadagnare l’equilibrio (inefficienza di mercato), possiamo introdurre un “lag” che sancisca il ritardo di un giorno tra l’individuazione del mispricing e la chiusura dell’operazione (es.: in t-2 osservo un titolo sottovalutato che compro in t-1 (ancora sottovalutato) e vendo in t); la regressione assume, così , la seguente forma:

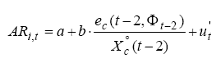(1.3.2b)

I risultati empirici prodotti dall’applicazione di tali regressioni al campione di dati sui BTP sono riportati nella tabella 7; si possono osservare le stime mediante la cross-section giornaliera e la cross-section settimanale, e per entrambe sono state stimate le due regressioni di cui sopra (Lag = 0 e Lag = 1):

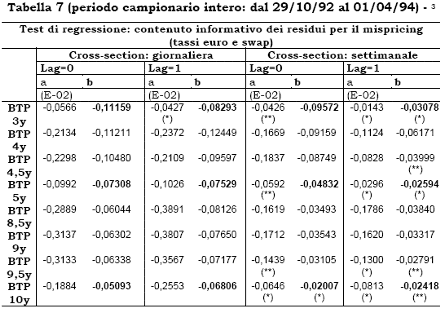
Se si osservano le stime di b, si può notare come il coefficiente sia quasi sempre negativo, ma mai con valori prossimi a –0.2; questo risultato ci porta a sottolineare la presenza di informazioni per il trading nei “pricing errors”, che tuttavia devono convivere con problemi di fitting che contaminano il segnale. Questo test di regressione, quindi, evidenzia un’utilità economica dei residui del modello, anche se tali risultati si sono dimostrati non eccezionali, soprattutto se confrontati con quelli ottenuti in un’applicazione analoga, al mercato belga, da Sercu e Wu (1997).

Ora, la considerazione del fatto che il periodo campionario scelto fosse caratterizzato da elevate turbolenze (tra la fine dell’inverno e l’inizio della primavera del ’93 la lira patisce una forte debolezza e soccombe sotto la forza del marco tedesco, con il cambio che supera le 1000 lire), con conseguenti performances di fitting non ottimali (limite congenito dei modelli uni-fattoriali), mi ha portato a considerare ed indicare in tale elevata volatilità la causa dei non buoni risultati delle regressioni. La verifica della validità o meno di tale affermazione è oggetto di analisi nella prossima sezione.

---

3 Test di significatività dei parametri: (*) = parametro statisticamente non significativo al 10%; (**) = parametro statisticamente non significativo al 5%.

Fulvio Pegoraro

Successivo: Test di regressione con mercato "moderato"

Sommario: Indice