Un aspetto più squisitamente econometrico riguarda il modello stocastico interpretativo delle aspettative sui rendimenti finanziari qualora queste dipendano dalla conoscenza dei valori delle quotazioni già verificatisi. Questa ovviamente appare come la situazione più realistica: ogni giorno sul mercato gli operatori conoscono quanto già successo e si creano delle aspettative per quanto accadrà domani.

Numerose verifiche empiriche hanno messo in evidenza che la serie storica dei rendimenti di molte serie finanziarie possiede, per alcuni aspetti, le caratteristiche di un modello stocastico noto in letteratura con il nome di rumore bianco (white noise). Assumendo per semplicità che un titolo non possieda dividendo, allora il suo rendimento è dato unicamente dal capital gain. Più precisamente se 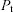rappresenta il prezzo del titolo, il suo rendimento 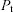è definito da:

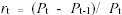
che può essere ben approssimato dalla differenza logaritmica3:

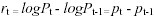
dove

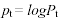
quindi

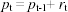
La formulazione appena data del prezzo 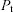descrive un comportamento chiamato passeggiata casuale (random walk) [4] che possiede particolari proprietà. Tra quelle rilevanti è opportuno menzionare:

. la varianza di pt non è costante nel tempo;

. la previsione (ovvero l'aspettativa), ottimale sulla base di un criterio abbastanza generale, di 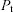un passo avanti (cioè di 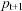), risulta essere semplicemente 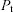, cioè si può scrivere

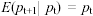
dove

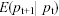
rappresenta appunto l'aspettativa del prezzo per il tempo t+1 condizionalmente all'informazione posseduta fino al tempo t. Questo risultato sembra per certi aspetti sconfortante: la migliore previsione per il prezzo di domani è il prezzo osservato oggi sul mercato. Il prezzo osservato oggi contiene tutta l'informazione necessaria a formare l'aspettativa degli operatori ed è una informazione disponibile a tutti. Questo risultato è coerente con l'ipotesi di mercato efficiente a cui hanno fatto riferimento importanti economisti come Samuelson e Fama;

. gli incrementi di prezzo, cioè i rendimenti, sono indipendenti gli uni dagli altri nel tempo ed hanno varianza costante (proprietà di stazionarietà). Ciò significa che essi sono indipendenti non solo dalle aspettative del prezzo (momento primo condizionale), ma anche dai momenti condizionali di ordine più elevato rispetto al
primo.

Formalmente il random walk è considerato come un particolare elemento della classe dei processi autoregressivi non stazionari. Nello sviluppo della modellistica, l'assunzione di un comportamento random walk è considerata troppo restrittiva per poter generare un'ampia classe di processi interpretativi del comportamento delle serie finanziarie. Questa limitazione è superata con la ricerca di una classe di processi che soddisfi alla condizione

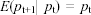
senza ulteriori restrizioni su altri parametri (i momenti condizionali superiori al primo) della loro distribuzione. Tale classe esiste ed è la classe dei processi martingala: un processo di tipo martingala ha necessariamente incrementi indipendenti o non correlati ma non è stazionario, è quindi compatibile con modelli stocastici non lineari capaci di interpretare particolari comportamenti dei momenti condizionali di ordine superiore al primo. Ad esempio, è stata proposta un'ampia classe di modelli detti con varianza condizionalmente autoregressiva (Autoregressive Conditionally Heteroskedastic - ARCH), fondata su una particolare struttura del secondo momento condizionale, che si è dimostrata spesso empiricamente adatta ad interpretare gli andamenti della volatilità dei prezzi.

[Sommario] [Successivo : I modelli Arch e Garch ]