Generalmente la statistica classica richiede che le variazioni dei prezzi siano normalmente distribuite. Uno dei motivi è che la distribuzione Normale (o gaussiana) è descrivibile ricorrendo a due soli parametri: la media e lo scarto quadratico medio (inteso come la radice quadrata della media aritmetica dei quadrati degli scarti dei valori osservati rispetto alla media, detta anche Deviazione Standard).

Quest'ultimo è lo strumento usuale per rappresentare la dispersione attorno alla media di una variabile casuale. Infatti, la probabilità di cogliere un'osservazione al di sotto o al di sopra della media dipende solo dallo scarto quadratico medio. Nelle serie storiche reali in campo economico e finanziario – dagli indici, ai rendimenti azionari, ai tassi di interesse – (ma anche in campo fisico), tuttavia, le distribuzioni dei rendimenti si presentano in forme diverse. I grafici in figura 3.1 mettono a confronto la distribuzione delle osservazioni di alcune serie storiche reali con quelle teoriche di una distribuzione Normale.

Essi fanno riferimento alla distribuzione delle variazioni percentuali a un giorno dell'indice Standard & Poor's 500 dal 4 gennaio 1928 al 25 aprile 2001 per un totale di 19.490 osservazioni; dell'indice COMIT Globale dal 2 gennaio 1973 al 29 dicembre 2000 per un totale di 7.028 dati e delle variazioni percentuali a un giorno delle quotazioni del titolo IBM al NYSE dal 2 gennaio 1962 al 29 dicembre 2000 per un totale di 9.805 osservazioni. Come si può notare in tutti e tre i casi la frequenza con cui si le osservazioni cadono negli intervalli considerati (dell'ordine di 0,1 Dev. Stand.), non è la stessa di quella di una distribuzione normale. Particolarmente significativo è il campione dell'indice S&P 500 che copre un periodo di circa 73 anni corrispondente a quasi ventimila giorni di contrattazioni.

Generalmente si fa notare che se si disponesse di un numero elevato di osservazioni la forma della distribuzione dovrebbe approssimare con maggiore precisione quella Normale. Nel caso considerato questa conclusione non sembra reggere, ma al contrario la forma della distribuzione dei dati tende a consolidare una propria forma caratteristica. I grafici delle figure 3.2 a, b, c, visualizzano graficamente la differenza tra la numerosità delle osservazioni (espresse in termini di variazioni percentuali) e la corrispondente distribuzione Normale teorica per sette diversi orizzonti temporali.

In tutti i casi si riscontra una distribuzione con la stessa forma, caratterizzata da un picco positivo (leptocurtosi) approssimativamente tra -1 e 1 deviazioni standard e la presenza di code più spesse rispetto a una Normale gaussiana. La tabella 3.1 riporta i dati specifici del confronto tra il campione di dati dello S&P 500 ed una Normale calcolata sullo stesso numero di osservazioni. Si può notare come, a partire da tre Dev. Stand., il campione presenti una numerosità superiore a quella prevista da una distribuzione Gaussiana.

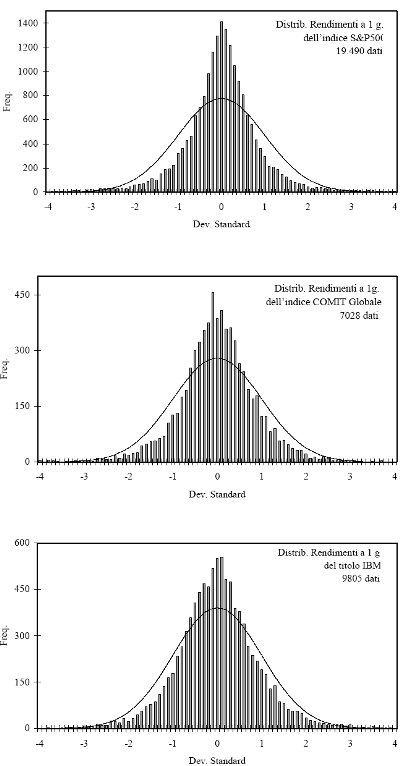
Figura 3.1 - Distribuzione di Frequenza delle variazioni percentuali a una giorno dell’indice Standard & Poor’s 500 (4 gennaio 1928 - 25 aprile 2001); dell’indice COMIT Gobale (2 gennaio 1973 - 29 dicembre 2000); del titolo azionario IBM quotato al NYSE dal 2 gennaio 1962 al 29 dicemebre 2000.

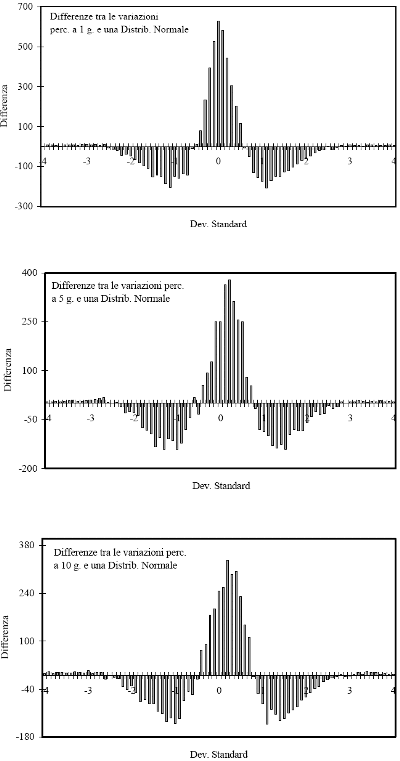
Figura 3.2a - Differenze tra le variazioni percentuali a uno, cinque e dieci giorni dello Standard & Poor's 500 e una distribuzione Normale di un'equivalente numerosità di dati. Per il confronto le variazioni percentuali dei campioni sono state standardizzate.

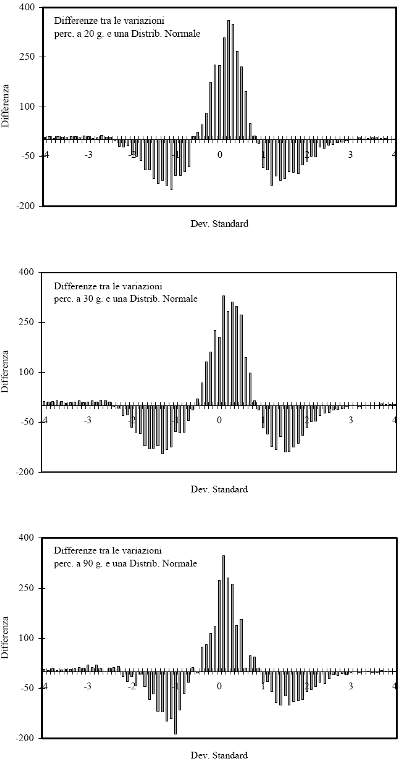
Figura 3.2b - Differenze tra le variazioni percentuali a venti, trenta e novanta giorni dello Standard & Poor's 500 e una distribuzione Normale di un'equivalente numerosità di dati. Per il confronto le variazioni percentuali dei campioni sono state standardizzate.

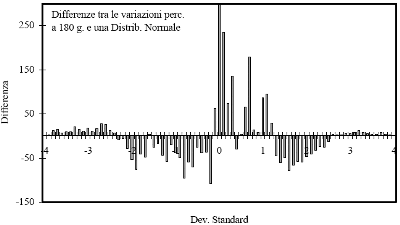
Figura 3.2c - Differenze tra le variazioni percentuali a centottanta giorni dello Standard & Poor’s 500 e una distribuzione Normale di un’equivalente numerosità di dati. Per il confronto le variazioni percentuali dei campioni sono state standardizzate.

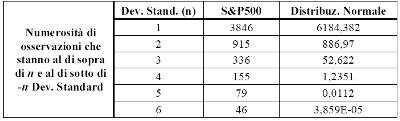
Tabella 3.1 - Numerosità delle variazioni percentuali a un giorno dello Standard & Poor's 500 che cadono nelle code della distribuzione per diverse ampiezze delle stesse. L'ampiezza di ogni coda è misurate dalla Deviazione Standard. Si noti come a partire da tre Dev. Stand. le code della distribuzione del campione sono sempre più spesse di quelle di una Normale.

La misura dello Skewness è pari a -0,1 (per una Normale Standard è zero) e la misura della Kurtosis è di 22,11 (per una Normale è 3). Il test di normalità di Jarque-Bera rifiuta, senza dubbio l'ipotesi di normalità della serie. Infatti produce un valore molto alto, vicino a trecentomila, quando il valore critico per un livello di significatività dell'un per cento è 9,21. Questo comportamento dei rendimenti ha delle implicazioni sul rischio.

La probabilità che si verifichi un evento di una certa rilevanza è maggiore di quella implicata da una Normale. In base ai dati disponibili per l'indice S&P 500, la probabilità che si verifichi un evento che discosti la variabile osservata dalla media, per esempio, di oltre tre variazioni standard, è in media nei sette casi di orizzonti considerati, 1,58 per cento, equivalente a circa sei volte quella prevista da una Normale (0,27 per cento).

Giancarlo Fabbro

Successivo: Caratteristiche statistiche delle serie storiche frattali II

Sommario: Indice