L'origine dell'esponenente di Hurst

Harold Edwin Hurst era un idrologo che lavorò al progetto di una diga sul fiume Nilo in Egitto agli inizi del ventesimo secolo. Il suo compito era quello di studiare un sistema di controllo della quantità di acqua contenuta in una diga, in modo che questa non fosse mai troppa o troppo poca. Il fattore principale che influenza il livello d'acqua in una diga è senza dubbio la quantità di pioggia caduta e, siccome usualmente si tende ad ipotizzare che tale quantità segua un random walk, Hurst decise di verificare se effettivamente il livello d'acqua nella diga, misurato in periodi di tempi successivi, seguiva veramente un andamento casuale.

Grazie ai dati raccolti dagli egiziani sulle piene del loro fiume nel corso di svariati secoli (dal 622 a.C. al 1469 d.C.), ebbe modo di notare che generalmente a ondate di piana più intense della media seguivano, con maggiore frequenza, altre ondate di piana di simile intensità e, al contrario, a ondate lievi, con maggiore probabilità ne seguivano altre ancora di lieve entità. Questo comportamento sembrava avere un andamento ciclico anche se la lunghezza dei cicli non era costante. Egli però, usando i metodi statistici standard, non riscontrò una significativa correlazione tra le osservazioni. Decise quindi di mettere a punto una propria metodologia di analisi che portò a dei risultati inaspettati.

L'analisi R/S

Albert Einstein, approfondendo gli studi sui moti browniano, scoprì che una particella che si muove in modo erratico copre una distanza che, in media, è funzione della radice quadrata del tempo per una costante, secondo la relazione:

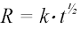(4.1)

dove R è la distanza coperta, t il tempo e k una costante.

Generalizzando, la 4.1 può essere riscritta in questo modo:

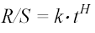(4.2)

Nella 4.2 k è ancora una costante, t è il tempo (espresso come successione di numeri reali) e H l'esponente di Hurst. Il termine R/S è dato dal rapporto tra il Range R e la deviazione standard (S) delle osservazioni del campione della serie storica in esame (perciò il nome Rescaled Range Analysis). In particolare il range R è ottenuto come differenza tra il massimo ed il minimo della sommatoria cumulata degli scarti dalla media delle osservazioni del campione considerato (la metodologia di calcolo sarà chiarita più avanti). La divisione per la deviazione standard consente di standardizzare la misura in esame permettendo il confronto fra i risultati di diverse analisi.

In generale R/S cresce all'aumentare di t secondo una legge esponenziale funzione di H. Questo è un primo legame della statistica di Hurst con i fenomeni frattali. I frattali sono oggetti le cui parti hanno dimensioni legate alla forma delle altre parti dell'oggetto stesso da una legge esponenziale (si ripensi agli esempi visti nel capitolo sui frattali). Nel caso delle serie storiche il fattore di scala è rappresentato da intervalli di tempo che crescono in ampiezza.

Con l'esponente di Hurst si possono classificare le serie storiche secondo il valore che H assume. Permette di distinguere una serie di dati la cui struttura è governata da un processo casuale, da una in cui tale processo non si può definire propriamente di tipo random walk. Inoltre non richiede alcuna restrizione sulla distribuzione dei dati in esame. Non richiede, per esempio, che la distribuzione si di tipo Normale, come avviene per altre statistiche che possono risultare distorte se tale assunzione non è coerente con la realtà dei dati. Il processo potrebbe quindi assumere un qualunque tipo di distribuzione senza incidere sulla validità dell'analisi R/S.

Mandelbrot (1997) ha dimostrato che H può assumere un valore compreso tra zero ed uno. In particolare si possono distinguere tre classificazioni: 1) H = ½; 2) 0 > H < ½; 3) ½ < H > 1.

Si esaminano di seguito le tre classificazioni di H.

1) H = ½ Quando H = ½ la 4.2 coincide con il caso particolare rappresentato dalla 4.1. In questa ipotesi la serie in esame segue un processo random walk. Il passato non influenza il futuro e non vi e memoria alcuna che influenzi la direzione del processo che non ha quindi una direzione "preferita" rispetto a quella seguita in precedenza. In altre parole il valore corrente della variabile, è l'unico dato utile per stimare la direzione che la stessa può prendere nell'istante immediatamente successivo.

2) 0 ≤ H < ½

Valori compresi in questo intervallo segnalano la presenza di un effetto antipersistente. Il sistema "copre" una distanza inferiore di quella coperta da un processo random walk. Ciò significa che la variabile tende a cambiare molto frequentemente la direzione. Semplificando, se il sistema assume una direzione positiva in un certo intervallo di tempo, è molto probabile che nell'intervallo successivo diventi negativa. Le serie di questo tipo tenderanno ad essere molto volatili a causa delle frequenti variazioni di valore.

3) ½ < H ≤ 1

In questo intervallo di valori, H segnalerà la presenza di una persistenza nella serie. Perciò se la variabile ha mantenuto un andamento crescente nel corso di un certo intervallo di tempo, è probabile che mantenga lo stesso segno nell'intervallo successivo. Questo comportamento prende il nome di effetto Joseph (Mandelbrot, 1983). Il nome deriva dalla storia biblica della previsione di sette anni di abbondanza seguiti da sette anni di carestia. In oltre, sistemi classificabili in questa categoria, sono caratterizzati da potenziali effetti catastrofici a causa degli improvvisi cambiamenti che li possono riguardare (Effetto Noah Mandelbrot, 1983 - riferendosi al diluvio universale).

Quanto più H si avvicinerà ad ½, tanto maggiore sarà il rumore che nasconde il processo. Quanto più si avvicinerà ad uno, tanto maggiore sarà la forza della persistenza. Si riscontrerà una correlazione di lungo termine positiva, ovverosia un effetto memoria che pervade qualsiasi scala temporale od orizzonte temporale. Il concetto che sta alla base di H riguarda la possibilità che le osservazioni siano dipendenti, non tanto nel breve termine, quanto nel lungo termine.

Ogni osservazione porterebbe memoria degli eventi passati. Gli effetti di tali eventi continuerebbero a farsi sentire, anche se in modo sempre più smorzato, sulle vicende future, anche se lontane nel tempo, e teoricamente all'infinito. In una concezione più ampia, un sistema che esibisca una statistica di Hurst, sarebbe il risultato di un continuo flusso di eventi interconnessi tra loro. Ciò che accade oggi teoricamente avrà ripercussioni sugli sviluppi futuri in modo permanente (Peters, 1994). La variabile tempo in questo contesto di analisi assume un'importanza fondamentale e non è possibile semplificare assumendo che il campione di dati in esame sia invariante rispetto al tempo. La correlazione di lungo termine su menzionata, può essere misurata dalla seguente relazione (Mandelbrot, 1997):

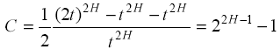(4.3)

Si noti come C sia indipendente da t ed esprime la correlazione tra le variazioni della variabile in un certo intervallo temporale con le variazioni della stessa variabile in intervalli temporali della stessa lunghezza che seguono o precedono il primo. Ovvero tra la media passata [X(t0) - X (-tn)]/n e la media futura [X(tn) - X (t0)]/n. In modo equivalente, con riferimento alle variazioni dei prezzi di un indice, di un titolo, ecc., C esprime la correlazione tra i rendimenti a un giorno con quelli, sempre a un giorno, misurati in passato e quelli che si rileveranno in futuro. Oppure la correlazione tra quelli a cinque giorni e quelli passati e futuri, sempre a cinque giorni, ecc. Teoricamente, quindi, può misurare la correlazione tra tutti gli incrementi temporali misurando la forza dell'effetto di memoria lunga con riferimento ad ogni scala temporale.

Per H = ½, C è pari a zero. Ovverosia, non vi è alcuna dipendenza tra le osservazioni nel lungo termine come nel breve, come è immaginabile che accada in un processo random walk (o browniano). Quando ½ < H > 1, C assume valori positivi dando la misura della forza dell'impatto trascinante del presente sul futuro; al contrario C è negativo quando 0 > H < ½.

Giancarlo Fabbro

Successivo: L'esponente di Hurst II

Sommario: Indice