Un'altra simulazione è stata compiuta su una seri di dati generati usando un algoritmo così articolato. Si sono generate venti sinusoidi di ampiezza e periodo variabili. Ad ogni sinusoide è stata aggiunta una componente positiva o negativa allo scopo di sollevarla o abbassarla rispetto all'asse orizzontale, ed una componete crescente in modo esponenziale. L'analisi è stata quindi effettuata prima sulla serie così generata, e successivamente sulla stessa dopo aver aggiunto una doppia componente di disturbo rappresentata da una serie casuale di valori normalmente distribuiti con media zero e varianza dieci, ed una serie casuale distribuita χ² moltiplicata per cinque.

La serie generata è composta da 1.150 osservazioni distribuite sulle venti sinusoidi che in media completano il ciclo ogni 57,35 osservazioni. In figura 4.7 sono visibili i grafici della serie con e senza la componente di disturbo. Osservando un porzione di entrambi i primi due grafici (osservazioni da trecento a cinquecento) si cogliere visivamente meglio la differenza tra i due casi. Applicando l’analisi R/S, in questi casi si riesce ad individuare il ciclo medio (MOP) là dove si immagina debba essere, cioè ad 1,76 log(57,35).

I grafici a) e b) mostrano il risultato dell'analisi applicata ai dati privi del disturbo. Come si può notare (evidenziato anche dalla retta di regressione chiara) nel punto richiamato si ha il cambiamento strutturale previsto, meglio visibile nel grafico b) specifico della statistica Vn . La stima di H è di 0,71 (Std. Error. 0,015; R²= 0,9795) evidenza della persistenza data dalla struttura sinusoidale della serie.

Clicca per ingrandire

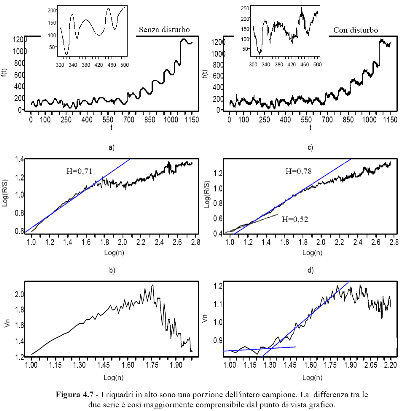
L'esito più interessante si ha passando all'analisi della serie comprensiva della componente di disturbo (grafici c)e d)) . Nonostante l'aggiunta della componente di disturbo la misura del ciclo medio non differisce in modo sensibile rispetto alla serie priva del rumore. La stima di H è salita a 0,78 (Std. Error 0,01; R²= 0,994) confermando la persistenza dell'andamento sinusoidale di lungo termine, ma l'analisi coglie anche la disposizione casuale dei dati nel breve termine. Infatti, osservando il grafico c) è possibile notare come il primo tratto (log(n)≤ 1,25) equivalente a circa 18 osservazioni) il coefficiente angolare della retta sia più basso e prossimo a ½ (stimato H = 0,52; Deviazione Std. 0,033; R² = 0,9731).

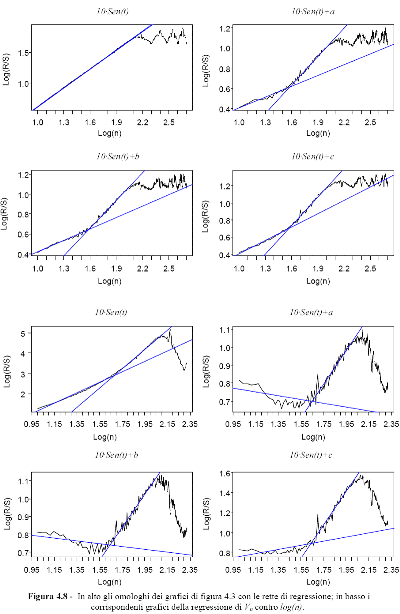
Conferma di questo comportamento si ha analizzando il grafico della statistica Vn che effettivamente per lo stesso intervallo mantiene un andamento mediamente costante. Solo in seguito presenta un andamento crescente fino al punto che individua il ciclo medio. Lo stesso comportamento, anche se in modo meno evidente, era già visibile nei grafici di figura 4.3 relativi alla sinusoide con i tre casi di disturbo di diversa tipologia (riproposti in figura 4.8 con le rette di regressione e i grafici delle statistiche Vn ). Infatti si può notare come i tre grafici in questione, abbiano un tratto iniziale (log(n)< 1,6) con una pendenza inferiore rispetto al tratto centrale.

Anche in quel caso l'analisi R/S coglie la struttura ciclica di base che emerge nel lungo periodo, mentre rileva la struttura casuale (random walk) che caratterizza la serie nel breve periodo. Le tabelle che seguono riportano le statistiche relative alla regressione del log(R/S)n contro il log(n) per la stima di H nei due tratti rilevanti (tabella 4.2) e la stima dei coefficienti angolari della rette dei grafici della statistica Vn (tabella 4.3). Per quanto riguarda la misura di H, questa rimane prossima a uno in tutti e quattro i casi.

L'ipotesi senza disturbo, effettivamente presenta una stima di H unitaria. La persistenza in un andamento sinusoidale è evidente e non può quindi sfuggire all'analisi. Anche dopo l'inclusione del rumore la stima rimane prossima a uno. Tutte le stime, inoltre, presentano un buon adattamento ed un'elevata significatività. In particolare le stime di H nel primo tratto sono inferiori a ½, quindi il comportamento è per l'appunto antipersistente poiché tale è la natura dell'interferenza usata.

Passando ai risultati delle stime della regressione di Vn contro il log(n) (tabella 4.3), si può avere la conferma del fatto che quando H < ½, la stima del coefficiente angolare della retta della regressione di Vn contro il log(n) è negativo; viceversa è positivo.

L'ultima osservazione che si vuole fare, riguarda la presenza di un picco all'altezza di log(n) = 1,7, visibile in quasi tutti grafici della figura 4.8 evidente soprattutto nei grafici della statistica 9 Ä . Il fatto che si presenti esattamente nello stesso punti in tutti e tre i casi con l'elemento di disturbo, è a favore dell'ipotesi che non si tratti di un segnale casuale. Tale valore, infatti, equivale ad n 50 che il numero di osservazioni per il quale ciclicamente una sinusoide di periodo cento, mantiene un andamento crescente e successivamente decrescente o viceversa.

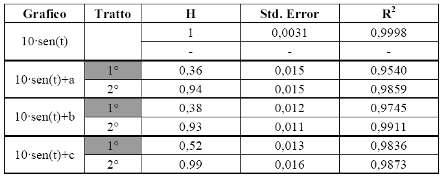
Tabella 4.2 - Stime di H per i dati usati per costruire i primi quattro grafici di figura 4.8

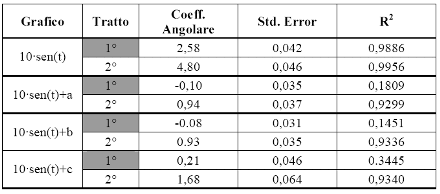
Tabella 4.3 - Stime dei coefficienti angolari della regressione di Vn contro il log(n) (secondi quattro grafici di figura 4.8).

Clicca per ingrandire

L'ultima prova è stata compiuta sui dati usati per costruire i grafici 2.6 del paragrafo 2.2.3 sulla funzione di Weierstrass. Come si ricorderà la funzione è caratterizzata da due parametri: 1 < V < 2 e λ >1.

È dimostrato che V è la dimensione frattale della funzione di Weierstrass (Falconer, 1990). Dunque stimando H, la dimensione frattale di f(t) deve essere pari a DG = 2 – H. Si sono quindi generate nove serie di 3.000 dati ciascuna mantenendo costante λ = 1,5 e variando s da 1,1 a 1,9. Quindi si è applicata l'analisi R/S ai dati così generati. I Risultati delle stime di H sono visibili in tabella 4.4. Come si evidenzia anche dal grafico, la stima è più lontana dal valore teorico agli estremi, mentre migliora per valori di s più vicini a 1,5.

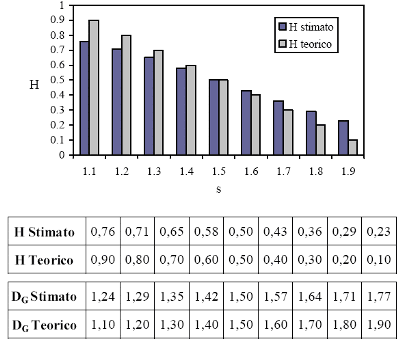
Tabella 4.4 - Stima dell’esponente di Hurst e della dimensione frattale per i grafici della funzione di Weierstrass, paragrafo 2.2.3.

Giancarlo Fabbro

Successivo: Appendice

Sommario: Indice