L'analisi R/S può essere utile anche nella rilevazione delle componenti periodiche che caratterizzano una serie storica. In particolare può misurare anche la durata media (Mean Orbital Period) dei cicli non periodici.

I cicli non periodici possono essere visti come una generalizzazione dei cicli periodici. Per esempio una sinusoide ha un ciclo periodico costante di 2π. Serie storiche con comportamenti casuali possono avere dei cicli periodici, tuttavia la loro durata varia in modo casuale in base ad una qualche distribuzione. Se questa ha media e varianza finite, potrà essere misurata anche la durata media dei cicli che saranno quindi non periodici.

Un processo FBM non rientra in queste ipotesi. Benché possa tendere ad oscillare entro un massimo ed un minimo, non esiste una durata media e quindi non vi si devono trovare cicli. Si ricordi, infatti, che un FBM cresce, in media, nel tempo secondo la legge t^H (0≤H≤1). Mandelbrot (1983) afferma, infatti, che quando si tratta di distribuzioni frattali l'esistenza di un ciclo non è necessariamente certa.

Dal punto di vista della rappresentazione grafica dell'analisi R/S, ciò significa che la disposizione dei dati del log(R/S)n contro il log(n) segue costantemente la retta di regressione senza deviarvi, ovvero non si rileva un cambio strutturale nei dati del log(R/S)n (come accade nella figura 4.2). In tale circostanza la stima di H è fatta considerando come dati della regressione tutti i valori di n = 10,11...[m/2]. Tuttavia lo stesso procedimento sarebbe errato se la serie in esame presenta un ciclo che si ripete ancorché non periodicamente, vale a dire presenta una memoria finita che comporta l'esaurimento dell'influenza che gli eventi indietro nel tempo, di oltre un certo periodo, hanno sugli eventi attuali (Peters, 1991).

Un cambio strutturale nei dati della regressione può quindi essere il sintomo dell'esistenza di cicli periodici o non periodici. Si considerino i grafici di figura 4.3. Riguardano l'analisi di una serie di mille dati dt con andamento sinusoidale: dt = 10.sen(t) con t compreso fra zero e 62,77 con incrementi di 2π/100. Con questo incremento il ciclo delle cento sinusoidi del campione si completa in cento osservazioni. Considerando il primo dei quattro grafici, si può notare come il logaritmo di (R/S)n cresce costantemente sino a quando il logaritmo di n non è uguale a circa due. Il logaritmo (in base dieci) di cento è infatti due. Da questo momento in poi il log(R/S)n smette di crescere. In questo caso i dati per la regressione sarebbero quindi tutti quelli compresi fra uno e due.

Click to enlarge image

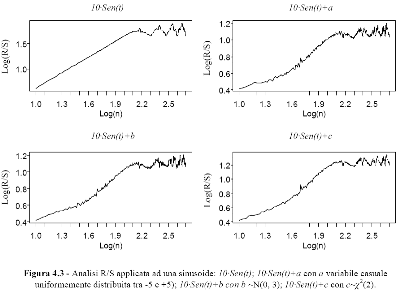
Gli altri tre grafici riguardano ancora una sinusoide alla quale, però, è stato aggiunto un elemento di disturbo. Nel primo dei tre casi il disturbo, rappresentato dalla variabile a, consiste nel sommare a 10.sen(t) un valore casuale uniformemente distribuito fra -5 e +5.

Per una sinusoide che oscilla tra -10 e +10, tale tipo di interferenza può significare una deviazione massima dal suo percorso ordinario, in aumento o in diminuzione, del 50 per cento. Negli altri due casi b è una variabile casuale normalmente distribuita con media zero e varianza tre; C una distribuzione χ² con due gradi di libertà. In tutti e tre i casi, per l'analisi R/S e irrilevante il tipo di distribuzione che caratterizza la serie o il disturbo. Il cambio strutturale si ha sempre in corrispondenza del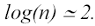

La ragione per cui il logaritmo di (R/S)n si comporta in questo modo in presenza di un ciclo, essenzialmente è dovuta al fatto che una volta che la funzione ha completato il primo ciclo, il range tra il massimo e il minimo ha raggiunto la sua misura massima. Non vi è quindi più differenza tra le seicento osservazioni del campione e le prime cento (Peters, 1994).

La capacità dell'analisi oggetto del lavoro, non si esaurisce nella possibilità di individuare solo il ciclo primario, ma anche cicli secondari fin tanto che questi sono in numero limitato. Per una verifica empirica si consideri la somma di tre sinusoidi di ampiezza e ciclo in progressione geometrica come nel caso seguente:

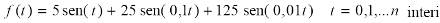(4.10)

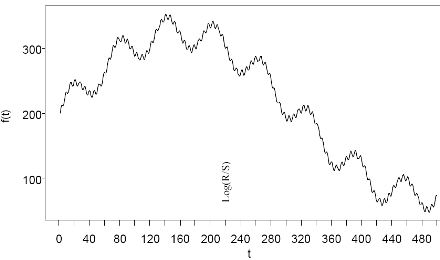
Figura 4.4 - Prime cinquecento osservazioni dei dati utilizzati per l’analisi R/S che genera i grafici di figura 4.5a, b.

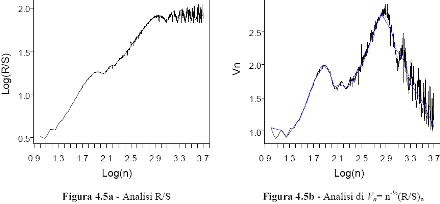
Il risultato è un tracciato di tre sinusoidi sovrapposte di ciclo rispettivamente 2π, 20π e 200π visibile in figura 4.4 che considera le prime 500 osservazioni delle diecimila a cui è stata applicata l'analisi (cioè t = 0,1,...,10000) La rappresentazione grafica dei risultati dell'analisi R/S (figura 4.5a) conferma la durata dei cicli impostata.

La fine di ciascun ciclo è segnata dall'interruzione della crescita costante nei dati del logaritmo di (R/S)n ovvero dal loro cambio strutturale che si nota chiaramente, nella figura 4.5a, in corrispondenza di circa 1,8 log ( 20π )e 2,8 log (200π), cioè in corrispondenza dei due cicli maggiori. Il ciclo minore di 2π non è visibile poiché inferiore a dieci osservazioni, quindi inferiore al log(10) = 1 che rappresenta il grado di "sensibilità" minima dell'analisi.

È interessante osservare come in corrispondenza del ciclo massimo (2,8 log(200π)),i valori del logaritmo di R/S, non crescono più, benché siano stati analizzati ben diecimila dati. L'individuazione del punto di cambio strutturale può rivelarsi difficile, in particolare in presenza di rumore nei dati. A tal fine per migliorare la leggibilità del grafico e individuare con maggiore precisione il punto di svolta, si può ricorrere ad una variante dell'analisi R/S così definita (Peters, 1994):

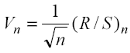(4.11)

Nell'ipotesi che il tasso di crescita di (R/S)n sia uguale a quello di V¯ n (H = ½), Vn sarebbe costante. Al contrario se (R/S)n cresce più velocemente della radice quadrata di n (H > ½), Vn è crescente, decrescente altrimenti (H < ½). Per tanto, quando un ciclo si chiude, il punto di massimo toccato dal rapporto 4.11 coincide con il momento in cui la persistenza relativa alla scala temporale di quel ciclo (20π) cessa ed ha inizio una nuova fase di crescita di (R/S)n che individua il successivo ciclo su una scala di valori diversa (200π).

La figura 4.5b mostra come i punti di cambio strutturale evidenti in figura 4.5a, vengano messi in rilievo dalla statistica Vn.

Per comprendere meglio quanto appena detto, si è presa in considerazione una funzione come quella che segue

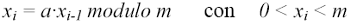(4.12)

Si tratta di un generatore di numeri che, benché originati da una funzione deterministica, all'apparenza produce una sequenza di numeri casuali, indipendenti ed uniformemente distribuite tra uno ed m-1. Si tratta, infatti, di un generatore di numeri pseudocasuali. Il principio è quello usato dai calcolatori per generare numeri casuali. L'apparenza è dovuta alla caratteristica di questi generatori. Infatti, ripetono esattamente la stessa sequenza dopo un certo numero di iterazioni dato che la varietà di resti dipende dai valori scelti per m ed a. Per ritardare il più possibile la ripetizione del ciclo, i parametri a ed m negli elaboratori sono impostati generalmente pari al numero primo più alto che l'elaboratore è in grado di trattare (quelli più comuni sono m = 2³¹-1, a = 7⁵; Gentle, 1998).

Per la simulazione si è scelto di porre a = 3, m = 2000 e x0 = 1(seed) allo scopo di ottenere un ciclo relativamente breve pari a cento. Il risultato è la sequenza casuale visibile nel grafico a) di figura 4.6 che per motivi di leggibilità considera solo i primi cento dati dei duemila usati nell'analisi. L'analisi R/S è stata inoltre compiuta sulla stessa serie dopo che è stata aggiunta una componente di disturbo rappresentata da valori casuali distribuiti normalmente con media nulla e varianza cento.

Tanto nel caso senza la componente di disturbo, quanto in quello con il disturbo, il cambio strutturale si ha a 2 = ORJ(100) (grafici a destra di figura 4.6). La stima dell'esponente di Hurst nel tratto a crescita constante è pari a 0,497 (Std. Error = 0,0082, R2 = 0,9763) nel caso senza disturbo, mentre scende a 0,386 (Std. Error = 0,0047, R2 = 0,987) nel secondo caso poiché l'aggiunta della componente di disturbo ha reso la serie antipersistente. Il grafico b) di figura 4.6, disegna il tracciato della statistica Vn per il campione di dati psèudocasuali senza la componente di disturbo. Come annunciato precedentemente, il rapporto tra (R/S)n e la V¯ n rimane costante nell'ipotesi che l'esponente di Hurst sia pari a ½, mentre decresce se H < ½.

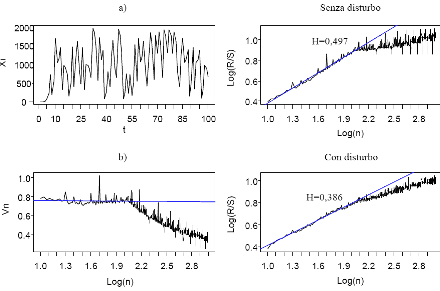
Figura 4.6 - Analisi R/S sui dati di un generatore di numeri psèudocasuali. La retta più chiara è la retta di regressione sul campione di dati che precede il momento di cambio strutturale.

 

Giancarlo Fabbro

Successivo: Ricerca di cicli periodici e non periodici II

Sommario: Indice