Cointegrazione tra variabili integrate dello stesso ordine

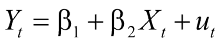
Si supponga di avere due serie ( X e Y ) non stazionarie e si supponga che le due variabili siano legate in termini lineari. Se l'ipotesi è corretta, la "divergenza" tra Y e X dovrebbe essere limitata.

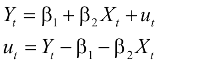
In termini tecnici, l'errore dell'equazione dovrebbe essere una serie stazionaria. Se questo accade, Y e X sono dette cointegrate.

Si può condurre un test di stazionarietà dei residui:

a) Stima OLS regressione statica

b) ADF residui

NB: La regressione con variabili non-stazionarie è ancora valida (se esse sono cointegrate). Cosa ottengo?

- Relazione di lungo periodo tra X _t e Y _t

- La relazione è stazionaria e converge (equilibrio stabile);

- Le discrepanze sono temporanee (equilibrium errors - disequilibrium errors).

- Tanti esempi empirici

ALCUNI RISULTATI TEORICI

Se X _t e Y _t sono cointegrati, lo sono anche X _t-k e Y _t .

Se X _t ~ I(1), X _t-kt X_t sono cointegrati.

Se Y _t ~ I(0), e X _t ~ I(1), Y _t = βX _t + u _t is a nonsense regression.

Se X _t e Y _t sono cointegrati, la relazione di cointegrazione può essere stimata con OLS (I parametri sono superconsistenti)

TESTING FOR COINTEGRATION

. Residual Based Tests

- Test for a unit root on residuals

. ADF, PP type Cointegration tests . Structural breaks?

. Tests using eigenvalues

- Johansen tests (based on VAR analysis)

DUE POSSIBILITA' DI STIMA IN PRESENZA DI COINTEGRAZIONE

Granger Representation theorem " Cointegration implies Error Correction Model (ECM)."

ES: Y _t ~ I (1), X _t ~ I (1), u _t = Y _t - βX _t ~ I (0)

Meccanismo a Correzione dell'errore; Engle-Granger two steps procedure

I MODELLI A CORREZIONE DELL'ERRORE

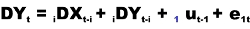
Che segno ci aspettiamo per il γ₁ ?

EG two steps procedure consente la stima delle elasticità di lungo periodo. La formulazione è del tipo:

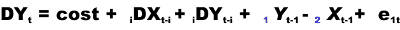
In ambedue I casi,

- Se X _t e Y _t non sono cointegrati, γ deve andare a zero

. - Se γ = 0, l'equazione diventa alle differenze.

- Se γ≠ 0, l'equazione alle differenze è mis-specified.

APPROCCI ALLA COINTEGRAZIONE

Punti deboli dell'approccio ECM e E&G:

. Può portare a risultati differenti!!

. Non permette la stima di vettori di cointegrazione multipli.

. L'approccio di Johansen supera questi problemi. Abbiamo bisogno di parlare di VAR

Prof. Paolo Mattana