Abbiamo generalizzato il modello classico per prendere in considerazione variabili indipendenti stocastiche; abbiamo chiaramente richiamato la necessità dell'indipendenza tra X e il termine di errore. I dati reali, tuttavia, spesso violano tale assunzione.

Abbiamo due possibilità teoriche:

- the contemporaneously uncorrelated case

i) presenza di variabili dipendenti ritardate

- the contemporaneously correlated case

i) "simultaneità"

ii) errori di misurazione

iii) distorsione da variabili omesse

Variabili dipendenti ritardate

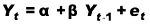
Se ritardiamo di un periodo otteniamo:

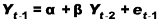
Ne deduciamo che Y _t dipende sistematicamente da e _t-1. Le due variabili stocastiche non sono perciò indipendenti.

Cosa succede in questo caso?

OLS E' DISTORTO (MA RESTA CONSISTENTE)

Dimostrazione: si parta dalla prova che beta è corretto e si supponga che X e e _t non siano indipendenti

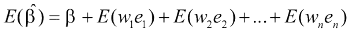
se ne deduce che

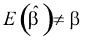
Continua tuttavia ad essere consistente

Dimostrazione: si parta dalla prova che beta è consistente:

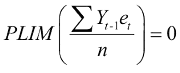
Infatti, non c'è nessuna ragione perchè il numeratore cresca o decresca (non c'è correlazione simultanea).

Torniamo ora al caso di simultaneous correlation Problema molto serio

OLS E' DISTORTO E NON CONSISTENTE

DIAGNOSI: Test di Hausman

RIMEDI:

i) Stime di modelli in "forma ridotta"

ii) Stime "IV" (con variabili strumentali)

MODELLI DI EQUAZIONI SIMULTANEE

- Esempio: domanda e offerta

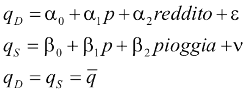
Cosa non va con le stime OLS in questo modello?

. Se otteniamo la " forma ridotta ", vediamo che abbiamo un problema di correlazione simultanea ( p è correlato con gli errori);

. P è una variabile dipendente (è determinato all'interno del modello)

. "pioggia" e "reddito", invece, possiamo effettivamente trattarli come esterni al modello

Prof. Paolo Mattana

Successivo: Violazioni delle ipotesi di indipendenza II

Sommario: Index