Non stazionarietà delle serie temporali

OBIETTIVI ULTIMA PARTE DEL CORSO

. Definire il concetto di non-stazionarietà delle serie temporali.

. Problema della regressione spuria (con più cognizione di causa).

. Distinguere tra trend-stationarity e difference-stationarity.

. Introdurre il concetto di "random walk".

. Descrivere i test per stabilire la presenza di "radici unitarie".

. Discutere le possibilità offerte dal concetto di Cointegrazione

. ECM

. Engle-Granger procedure

PROCESSI NON STAZIONARI

- La maggior parte delle serie economiche mostra andamenti col trend (crescente o decrescente).

- Per es: PIL, consumi, capitale, indici di prezzo..

- Perchè l'analisi di regressione possa essere condotta in termini corretti abbiamo bisogno di dati stazionari.

- Come possiamo procedere?

DEFINIZIONE DI STAZIONARIETÀ

- La stazionarietà si riferisce alle caratteristiche del processo stocastico sottostante che ha generato la serie temporale.

- Quando le caratteristiche del processo stocastico cambiano nel tempo abbiamo un processo non stazionario.

- Ci concentriamo sono la media, la varianza e le covarianze.

- Se una serie è stazionaria possiamo utilizzare la sua storia passata (per mezzo di un'equazione con coefficienti fissi) per prevedere il suo comportamento futuro (ricordate I processi AR?).

- Se una serie non è stazionaria dobbiamo procedere ad una trasformazione che induca stazionarietà

Si consideri una serie temporale, Y _t , con T osservazioni { y ₁ , ... , y _T}

Covariance Stationarity : un processo stocastico, Y _t è covariance- stationary se soddisfa ai seguenti requisiti:

1)

- Una serie stazionaria deve avere media costante

- Deve tendere ad una media costante.

- Il valore atteso sarà invariante nel tempo.

- Esempio di serie non stazionaria

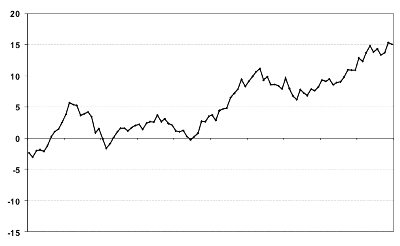
2)

. Una serie stazionaria deve avere varianza costante . Una serie non stazionaria ha una varianza non costante (che tende ad infinito). Provate infatti a tracciare la media di una serie temporale come quella rappresentata nella diapositiva precedente ...e calcolate la varianza..

PROBLEMA: La prova di consistenza dello stimatore OLS è ancora valida?

3)

. La covarianza tra le osservazioni dipende solo da quanto esse siano lontane; . Non tende a crescere o a decrescere con t; . Immaginatevi cosa succederebbe se il coefficiente di autocorrelazione del primo ordine dipendesse da t.

ALCUNE UTILI DEFINIZIONI

- Yt è detta integrata di ordine 0, I (0) se è stazionaria;

- Yt è integrata di ordine d , I ( d ) quando non è stazionaria e può essere resa I(0) dopo d differenziazioni.

- Le serie macroeconomiche e finanziaria sono spesso I (1).

- Queste serie differenziate una volta portano a variabili stazionarie

- NB: Se le serie I(1) sono espresse in termini logartimici, la loro differenza prima trasforma le variabili in termini di tassi di crescita.

Prof. Paolo Mattana