Non stazionarietà delle serie temporali I

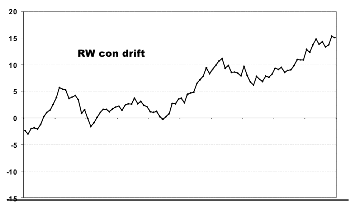
Le proprietà di un RW DRIFT

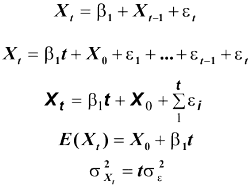
La prima condizione di non stazionarietà è violata La seconda condizione per non stazionarietà è violata

Se calcoliamo le differenze prime di un RW abbiamo:

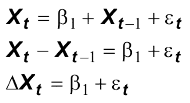
Si determini ora la media, la varianza e le covarianze della variabile trasformata. Abbiamo una serie stazionaria.

Una serie che può essere resa stazionaria per mezzo del calcolo delle differenze prime è chiamata difference-stationary (DSP) process or I(1).

TREND AND DIFFERENCE STATIONARY PROCESSES

Abbiamo imparato che esistono 2 tipi di serie non stazionarie:

-una stazionarizzabile con differenze prime (DSP process)

- una stazionarizzabile con detrendizzazione deterministica

- importante distinguere: svilupperemo test a questo scopo

Il problema consiste nel fatto che I due tipi di processo portano a risultati ben diversi nel lungo periodo. E' difficile capire da ispezione visiva

Un TSP è:

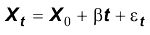
Un DSP è:

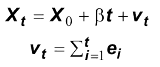
. I due processi sembrano uguali tranne per il fatto che il termine d' errore v _t è chiaramente non stazionario [avendo la varianza pari a s ²t (in una serie campionaria)]

NB: Perchè il termine di errore non è white noise?

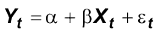
a) Si consideri un modello bivariato

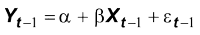
b) Si consideri ora un singolo ritardo

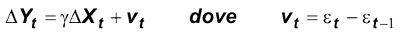
c) si sottraggano le equazioni:

. L'errore nell'equazione alle differenze è un processo MA(1) process (che è autocorrelato).

. Le stime OLS sono consistenti (sebbene inefficienti).

. Granger e Newbold (1974) hanno dimostrato che la stima dell'equazione alle differenze non distorce I test di significatività.

Prof. Paolo Mattana